Умовний екстремум для функції двох змінних

Нехай на відкритій множині 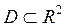задано функцію , змінні якої задовольняють рівнянню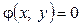

Рівняння 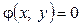називають рівнянням зв’язку.

Точку 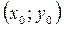називають точкою умовного строгого максимуму функції відносно рівняння зв’язку 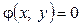, якщо існує такий окіл точки 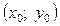, для всіх точок якого 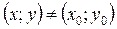, що задовольняють рівняння зв’язку, справджується нерівність .

Якщо за таких умов виконується 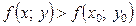, тоді точку 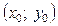називають точкою умовного строгого мінімуму функції при обмеженнях .

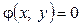Аналогічно вводяться поняття нестрогого умовного екстремуму.

Точки умовного максимуму та мінімуму називають точками умовного екстремуму. Умовний екстремум інколи називають відносним екстремумом.

Якщо рівняння зв’язку 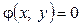можна розв’язати відносно змін­ної y, наприклад, , тоді дослідження функції на умовний екстремум при обмеженні 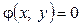зводиться до дослідження на звичайний екстремум функції однієї змінної x:

.

Приклад. Знайти умовний екстремум функції z = xy відносно рівняння зв’язку x + y = 6.

Розв’яжемо рівняння зв’язку відносно змінної y:

y= 6 – x

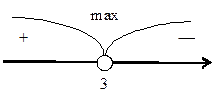
Підставимо знайдене значення y у вираз для z та зведемо задачу до дослідження на безумовний екстремум функції z = x(6 - x), 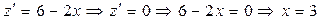. Таким чином, задана функція має умовний екстремум у точці (3; 3).

Дата добавления: 2014-01-15