Тригонометрична форма запису комплексних чисел

План.

1. Означення комплексного числа (*).

2. Дії над комплексними числами (**).

3. Тригонометрична форма комплексного числа (**).

4. Дії з комплексними числами в тригонометричній формі. Формула Муавра (**).

5. Корінь n- го ступіня з комплексного числа (**).

6. Формула Ейлера (*).

22.1 Означення комплексного числа і уявної одиниці

Число a + bί, де a,b – будь-які дійсні числа, ί – уявна одиниця, називається комплексним числом (a – дійсна частина, b – уявна частина комплексного числа, а ί – коефіцієнт при уявній частині).

Число, квадрат якого дорівнює , позначають літерою ί – називають уявною одиницею (ί – перша буква латинського слова imaginarius – уявний).

Тобто, для символу виконується рівність:

ί ² = 1

Означення: з апис a + bί називають алгебраїчною формою комплексного числа.

Часто комплексне число позначають літерою Z і записують Z = a + bi.

Комплексні числа – це розширення числової системи дійсних чисел. Позначаються вони літерою С. Множина дійсних чисел є частиною (підмножиною) множини комплексних чисел.

Означення: числа a + bί і a - bί, дійсні частини яких рівні, а коефіцієнти при уявих частинах рівні за модулем, але протилежні за знаком, називають спряженими. Можна сказати простіше: числа a + bί і a - bί, які відрізняються лише знаком уявної частини, називають спряженими.

Означення: два числа a + bί та -a - bί, сумма яких дорівнює 0, називають протилежними.

У множині дійсних чисел справедлива рівність a + 0 = a. У множині комплексних чисел нулем є число 0 + 0ί. Справді, яке б не було число, справедлива рівність

(a + b ί) + (0+0 ί) = (a +0) + (b +0) ί = a + b ί

22.2 Дії над комплексними числами.

Означення: сумою двох комплексних чисел a + bί і c + dί називається комплексне число (a + c) + (b + d)ί.

Приклади. Виконати додавання комплексних чисел:

1) (3+2ί) + (-1-5ί) = (3-1) + (2-5)ί = 2-3ί

2) (4-5ί) + (2-ί) = (4+2) + (-5-1)ί = 6-6ί

3) (2+3ί) + (6-3ί) = (2+6) + (3-3)ί= 8

4) (10 – 3ί) + (-10+3ί) = (10-10) + (-3+3)ί = 0

Означення. Різницею двох комплексних чисел Z ₁ = a + bί і Z ₂ = c + dί називається таке комплексне число Z = (а-с)+(b-d)ί.

Приклади: Виконати віднімання комплексних чисел.

1) (3+4ί) – (1+2ί) = (3-1) + (4-2)ί = 2 + 2ί

2) (-5+2ί) – (2+ί) = (-5-2) + (2-1)ί = -7+ί

3) (6+7ί) – (6-5ί) = (6-6) + (7+5)ί = 12ί

Означення. Добутком двох комплексних чисел Z ₁ = a + bί і Z ₂ = c + dί називається комплексне число z = (ac - bd) + (ad + bc)ί.

Приклади: Виконити множення комплексних чисел.

1) (4-5ί)(3+2ί) = 12+8ί -15ί -10ί²= 12+10-7ί =22-7ί

2) (2-ί)(-5) = -10+5ί

3) (-4-3ί)(-6ί) = -18+24ί

Означення. Часткою комплексних чисел Z ₁ = a + bί і Z ₂ = c + dί називається таке комплексне число:

Приклади. Знайти частку комплексних чисел.

1) (2+5ί)/(3-2ί) = (2+5ί)(3+2ί)/(3-2ί)(3+2ί) = (-4+19ί)/13 = -4/13+19ί/13

2) (3+ί)/ί = (3+ί)(-ί)/ί = 1-3ί

Кожному комплексному числу a + bί поставимо у відповідність точку М (a;b) координатної площини, тобто точку, абсциса якої дорівнює дійсній частині комплексного числа, а ордината – коефіцієнту уявной частини. Кожній точці М (a;b) координатної площини поставимо у відповідність комплексне число.

Очевидно, що така відповідність є взаємно однозначною. Вона дає можливість інтерпретувати комплексні числа як точки деякої площини, на якій вібрано систему координат. Координатну площину називають при цьому комплексною, вісь абсцис – дійсною віссю, бо на ній розміщені точки, що відповідають комплексним числам a + 0ί, тобто відповідають дійсним числам. Вісь ординат називають уявною віссю – на ній лежать точки, які відповідають уявним комплексним числам 0+ bί.

Модулем комплексного числа Z = a + bί називається число: r =. Позначимо α кут, який утворює вектор 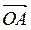з додатним напрямом осі Ох. Числове значення кута α, виміряного в радіанах, називається аргументом комплексного числа a + bί. Значення аргументу, взяте в межах першого кола, тобто від 0 до 2π, називається головним. Головне значення аргументу комплексного числа можна визначити з рівності tg α = b/a. Справді, за знаками a i b можна встановити, в якій четверті міститься кут α, і за величиною tg α, використовуючи таблиці, знайти величину кута α.

Вираз Z = r cos α + ί r sin α = r (cos α + ί sin α) називається тригонометричною формою комплексного числа.

Приклад. Подати в тригонометричній формі число – 3 + 2 і.

Маємо: ,

Тангенс від’ємний, отже, кут треба шукати в ІІ або IV чверті.

Далі: а = – 3 і b = 2 синус буде додатний, а косинус — від’ємний, тобто буде кутом ІІ чверті. За таблицями знаходимо: = 146° 18¢, а тому:

.

22.4 Дії з комплексними числами в тригонометричній формі. Формула Муавра.

Якщо задані два числа:

Z₁ = r₁ (cos α₁ + + ί sin α₁) і Z₂ = r₂ (cos α₂ + + ί sin α₂)

Тоді: Z₁ Z₂ = r₁r₂ (cos (α₁ + α₂) + ί sin (α₁ + α₂));

= (cos (α₁ – α₂) + ί sin (α₁ – α₂)).

При будь – якому натуральному n:

Z ⁿ = (cos α + ί sin α) ⁿ = cos nα + ί sin nα.

Приклад.

і .

Тоді:

a=12(cos55°+i sin55°) і b=3(cos35°+ +i sin 35°).

Тоді

Знайдемо куб число a = 2 (cos 20° + i sin 20°).

Маємо:

.

22.5 Корінь n -го ступеня з комплексного числа.

Корінь n – го ступеня з числа Z =r (cos α + ί sin α) обчислюють за формулою

ω_k =(cos + ί sin ), де k – ціле число.

Підставляючи замість k значення 0, 1, 2… n – 1, дістанемо n різних значень кореня.

Дата добавления: 2014-01-15