
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Суматори
|
|
|
|
Арифметичним суматором називається комбінаційна схема, яка призначена для додавання двох однорозрядних двійкових чисел.
Арифметичні суматори входять до складу так званих арифметико-логічних пристроїв (АЛП) мікропроцесорів (МП), де вони використовуються як для додавання двійкових чисел, так і для формування фізичної адреси комірки пам’яті.
Суматори класифікують по різних ознаках.
У залежності від системи числення розрізняють: двійкові; двійково-десяткові (у загальному випадку двійково-кодовані); десяткові.
По кількості одночасно оброблюваних розрядів чисел, що додаються: однорозрядні; багаторозрядні.
По числу входів і виходів однорозрядних двійкових суматорів:
w 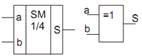 чвертьсуматори (елементи “сума по модулю 2”; елементи “виключаюче АБО”), що характеризуються наявністю двох входів, на які подаються два однорозрядних числа, і одним виходом, на якому реалізується їхня арифметична сума в поточному розряді;
чвертьсуматори (елементи “сума по модулю 2”; елементи “виключаюче АБО”), що характеризуються наявністю двох входів, на які подаються два однорозрядних числа, і одним виходом, на якому реалізується їхня арифметична сума в поточному розряді;
w 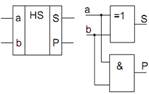 напівсуматори, що характеризуються наявністю двох входів, на які подаються однойменні розряди двох чисел, і двох виходів: на одному реалізується арифметична сума в даному розряді, а на іншому перенос у наступний (старший) розряд;
напівсуматори, що характеризуються наявністю двох входів, на які подаються однойменні розряди двох чисел, і двох виходів: на одному реалізується арифметична сума в даному розряді, а на іншому перенос у наступний (старший) розряд;
w 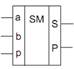 повні однорозрядні двійкові суматори, що характеризуються наявністю трьох входів, на які подаються однойменні розряди двох чисел, що складаються, і переніс з попереднього (молодшого) розряду, і двома виходами: на одному реалізується арифметична сума в даному розряді, а на іншому переніс у наступний (старший) розряд.
повні однорозрядні двійкові суматори, що характеризуються наявністю трьох входів, на які подаються однойменні розряди двох чисел, що складаються, і переніс з попереднього (молодшого) розряду, і двома виходами: на одному реалізується арифметична сума в даному розряді, а на іншому переніс у наступний (старший) розряд.
 По способу представлення й обробки чисел, що додаються, багаторозрядні суматори поділяються на:
По способу представлення й обробки чисел, що додаються, багаторозрядні суматори поділяються на:
w послідовні, у яких обробка чисел ведеться по черзі, розряд за розрядом на тій самій елементній базі;
w паралельні, у яких доданки додаються одночасно по всіх розрядах, і для кожного розряду є своя елементна база.
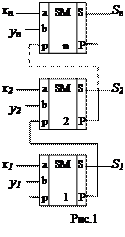
На рисунку 1 приведена схема n-розрядного паралельного суматора. X=x1x2…xn, Y=y1y2…yn - X i Y – n-розрядні додатні, S=s1s2…sn - результат додавання.
Чвертьсуматор, синтез схеми
Найпростішим двійковим сумуючим елементом є чвертьсуматор.
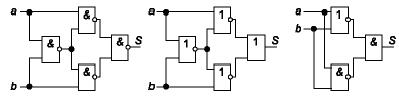
Походження назви цього елемента випливає з того, що він має в два рази менше виходів і в два рази менше рядків у таблиці істинності в порівнянні з повним двійковим однорозрядним суматором. Найбільш вживані назви: елемент “сума по модулю 2” і елемент “виключаюче АБО”. Схема (рис. 2) має два входи а і b для двох доданків, що додаються, й один вихід S для суми. Роботу її відображає таблиця істинності (табл. 1), а відповідне рівняння має вигляд: S=a̅b+ab̅=a⊕b
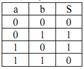 табл.1
табл.1 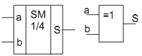 Рис.2
Рис.2
Синтезуємо схеми чверьсуматора в базисі І-НЕ, АБО-НЕ, І АБО НЕ.
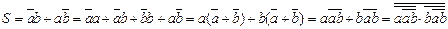
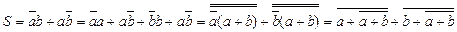
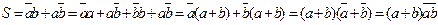
Напівсуматор (рис. 3) має два входи a і b для двох чисел, що сумуються і два виходи: S – сума, P – переніс. Позначають напівсуматор буквами HS (half sum – напівсума). Роботу його відображає таблиця істинності (табл. 2),
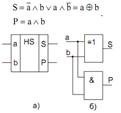 Рис.3
Рис.3 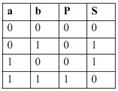 Табл.2
Табл.2
З рівнянь випливає, що для реалізації напівсуматора потрібно один елемент “виключаюче АБО” і один двовходовий елемент І (рис.2).
Повний однорозрядний двійковий суматор.
Повний однорозрядний двійковий суматор (рис. 4) має три входи: a, b для двох доданків і p для переносу з попереднього (молодшого) розряду і два виходи: S – сума, P – переніс у наступний (старший) розряд. Позначають повний двійковий суматор буквами SM. Його роботу відображає таблиця
істинності (табл. 3).
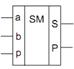 Рис.4
Рис.4 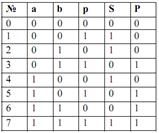 Табл.3
Табл.3
Записуємо рівняння виходів для S і для P, після чого складаємо принципову схему. S=(a̅ b+a b̅)p̅+(a̅ b̅+ab)p; P=(a+b)p+ab
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 700; Нарушение авторских прав?; Мы поможем в написании вашей работы!