Закони додавання і множення

1) Закон існування і єдиності суми.

З означення дробу і означення дії додавання невід’ємних раціональних чисел та закону існування суми і добутку натуральних чисел випливає, що дія додавання дробових чисел завжди здійсненна, тобто, що сума невід’ємних раціональних чисел завжди існує і є число невід’ємне і раціональне.

Наприклад. 1)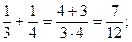

2)

У цих прикладах знайдено суму, користуючись означенням. Проте дроби 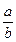і можна замінити еквівалентними їм дробами із спільним знаменником по-різному. Чи не зміниться від цього їх сума? Наприклад, дроби 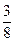і простіше додати, звівши до найменшого спільного знаменника:

2) Переставний закон: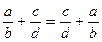

Доведення.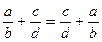

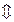
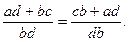
Беручи до уваги переставний закон додавання і множення натураль­них чисел, легко зробити висновок про тотожність цих виразів.

3) Сполучний закон:

Доведення.

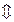
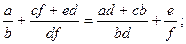
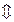
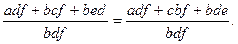
Ці вирази тотожно рівні. Оскільки всі перетворення еквівалент­ні, то і вихідна рівність є тотожністю.

Дія множення в множині невід’ємних раціональних чисел має ті самі властивості, що й множення натуральних чисел:

1) Існування і єдиність добутку: які б не були невід’ємні раціональні числа 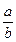, , завжди існує невід’ємне раціональне число 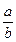· , що є їх добутком, і до того ж єдине.

2) Комутативний (переставний) закон: від зміни місць співмножників значення добутку не змінюється: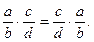

Доведення. Виконаємо дії у правій і лівій частинах рівності:

Оскільки для множення цілих невід’ємних чисел має місце комутативний закон, можна зробити висновок, що ці дроби рівні.

3) Асоціативний (сполучний) закон: окремі співмножни­ки можна сполучати в будь-які групи, а потім перемножати. Від цього значення добутку не зміниться: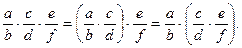

4) Монотонність множення: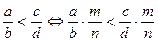

5) Дистрибутивний (розподільний) закон відносно до­давання і віднімання:

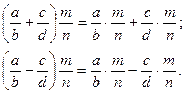
Приклади:

1)

2)

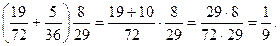
Дата добавления: 2014-01-15