Л.2. История психологии труда

4.

3.

Мультипликативная модель

Смешанная модель

П = VРП (Ц-С)

Пп = VРПп (Цп-Сп) ∆Пvрп=Пусл₁-Пп

Пусл₁ = VРПф (Цп-Сп) ∆Пц=Пусл₂-Пусл₁

Пусл₂ = VРПф (Цф-Сп) ∆Пс=Пф-Пусл₂

Пф = VРПф (Цф-Сф)

Используя способ цепной подстановки, следует придерживаться следующей последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого.

Метод абсолютных разниц является одной из модификаций элиминирования. Как способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и смешанных моделях типа: у=а(в-с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.

ВП=ЧР*Д*П*ЧВ

ВПп=ЧРп*Дп*Пп*ЧВп

∆ ВПчр= (ЧРф-ЧРп)*Дп*Пп*ЧВп

∆ ВПд= ЧРф*(Дф-Дп)*Пп*ЧВп

∆ ВПп= ЧРф*Дф*(Пф-Пп)*ЧВп

∆ ВПчв= ЧРф*Дф*Пф*(ЧВф-Чп)

ВП ф= ЧРф*Дф*Пф*ЧВф

∆ ВПобщ =∆ ВПчр+ ∆ ВПд + ∆ ВПп +∆ ВПчв

∆ ВПобщ = ВП ф - ВПп

Метод относительных разниц, как и предыдущий, применяется для измерения факторов на прирост результативного показателя только в мультипликативных моделях и комбинированных типа у=а(в-с). Он значительно проще способа цепных подстановок в тех случаях, когда исходные данные содержат уже определенные ранее относительные отклонения факторных показателей в процентах или коэффициентах.

ВП=ЧР*Д*П*ЧВ

∆ЧР = (ЧРф-ЧРп) / ЧРп

∆Д = (Дф-Дп) / Дп

∆П = (Пф-Пп) / Пп

∆ЧВ = (ЧВф-ЧВп) / ЧВп

ВПп=ЧРп*Дп*Пп*ЧВп

∆ ВПчр= ВПф*∆ЧР

∆ ВПд= (ВПф + ∆ ВПчр)*∆Д

∆ ВПп= (ВПф + ∆ ВПчр + ∆ ВПд)*∆П

∆ ВПчв= (ВПф + ∆ ВПчр + ∆ ВПд +∆ ВПп)*∆ЧВ

ВП ф= ЧРф*Дф*Пф*ЧВф

∆ ВПобщ =∆ ВПчр+ ∆ ВПд + ∆ ВПп +∆ ВПчв

∆ ВПобщ = ВП ф - ВПп

Преимущественно этого способа в том, что при его применении не обязательно рассчитывать уровень факторных показателей. Достаточно иметь данные о процентах выполнения плана по валовой продукции, численности рабочих и количеству отработанных ими дней и часов за анализируемый период.

В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными и смешанными моделями. Рассмотрим алгоритм расчета показателей способом пропорционального деления на примере:

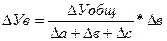
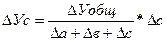
Элиминирование как способ детерминированного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.

Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа у=а/åх. Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними пропорционально изолированному их воздействию на результативный показатель. Рассмотрим алгоритм расчета влияния факторов, используя различные виды факторных моделей:

1. У=А*В

∆У_А= ∆А*В₀ + 1/2∆А*∆В

∆У_В= ∆В*А₀ + 1/2∆А*∆В

2. У=А*В*С

∆У_А= 1/2∆А(В₀С₁ + В₁С₀) + 1/3∆А∆В∆ С

∆У_В= 1/2∆В(А₀С₁ + А₁С₀) + 1/3∆А∆В∆ С

∆У_С= 1/2∆С(А₀В₁ + А₁В₀) + 1/3∆А∆В∆ С

Результаты расчетов те же, что и при использовании предыдущего способа.

Стохастический анализ – это метод решения широкого класса задач статистического оценивания. Он предполагает изучение массовых эмпирических данных путем построения моделей измерения показателей за счет факторов, не находящихся в прямых связях, в прямой зависимости и взаимообусловленности. Стохастическая связь существует между случайными величинами и проявляется в том, что при измерении одной из них меняется закон распределения другой.

Стохастическое моделирование можно применять в анализе хозяйственной деятельности, если есть возможность составить совокупность наблюдений. Моделирование ведется методами математической статистики, которые позволяют исследовать опосредованные причинно-следственные связи показателей производственно-хозяйственной деятельности с факторами и условиями производства. Детерминированное моделирование в данном случае не всегда возможно. С помощью математико-статистических приемов можно обойтись без специальных экспериментов.

В экономическом анализе выделяются следующие наиболее типичные задачи стохастического анализа:

изучение наличия и тесноты связи между функцией и факторами, а также между факторами;

ранжирование и классификация факторов экономических явлений;

выявление аналитической формы связи между изучаемыми явлениями;

сглаживание динамики изменения уровня показателей;

выявление параметров закономерных периодических колебаний уровня показателей;

изучение размерности (сложности, многогранности) экономических явлений;

количественное изменение информативных показателей;

количественное изменение влияния факторов на изменение анализируемых показателей (экономическая интерпретация полученных уравнений).

Стохастическое моделирование и анализ связей между изученными показателями начинаются с корреляционного анализа. Корреляционная связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений.

Корреляция состоит в том, что средняя величина одного ив признаков изменяется в зависимости от значения другого. Признак, от которого зависит другой признак, принято называть факторным. Зависимый признак именуют результа­тивным.

Применение корреляционного анализа позволяет решить следующие задачи:

1) определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), это, значит, определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

2) установить относительную степень зависимости результативного показателя от каждого фактора.

Исследование корреляционных соотношений имеет огромное значение в АХД. Это проявляется в том, что значительно углубляется факторный анализ, устанавливается место и роль каждого фактора в формировании уровня исследуемых показателей, углубляются знания об изучаемых явлениях, определяются закономерности их развития и как итог – точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятий и более полно определяются внутрихозяйственные резервы.

Для того, чтобы убедиться в точности (надежности) уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для это используется коэффициенты множественной корреляции и детерминации. Например, величина коэффициента множественной корреляции составляет 0,93, это означает, что в 93 случаях из 100 выбранные факторы влияют на значение результативного. Величина коэффициента детерминации равна 0,871. Это показывает, что учтенные факторы на 87,1 % объясняют изменение результативного показателя.

Исходя из этого, уравнение корреляции можно использовать для практических целей:

А) оценки результатов хозяйствования;

Б) расчета влияния факторов на прирост результативного показателя;

В) подсчета резервов повышения уровня исследуемого показателя;

Г) планирования и прогнозирования его величины.

Оценка деятельности организации по использованию имеющихся возможностей проводится сравнением фактической величины результативного показателя с теоретической (расчетной), которая определяется на основе уравнения множественной регрессии.

2.1. Представления о труде в древности и в эпоху феодализма

2.2. История зарубежной психологии и социологии труда

2.3. История отечественной психологии труда

2.4. Общие тенденции в развитии представлений о труде

Дата добавления: 2014-01-15