Симплексный метод

Выше были рассмотрены основные теоремы ЛП. Из них следует, что если ЗЛП имеет оптимальное решение, то оно соответствует хотя бы одной точке многогранника решений и совпадает хотя бы с одним из допустимых базисных решений системы ограничений. Там же мы рассмотрели, что путем решения любой ЗЛП является перебор конечного числа допустимых базисных решений системы ограничений и выбор среди них того, на котором функция цели принимает оптимальное значение. Геометрически надо перебрать все угловые точки многогранника решений. Трудно осуществить, т.к. для реальных задач число ДБР хоть и конечно, но м.б. велико.

Число перебираемых ДБР можно сократить, если производить перебор не беспорядочно, а с учетом изменений линейной функции, т.е. добиваясь, чтобы каждое следующее решение было «лучше» (или, по крайней мере, «не хуже») предыдущего по значению целевой функции.

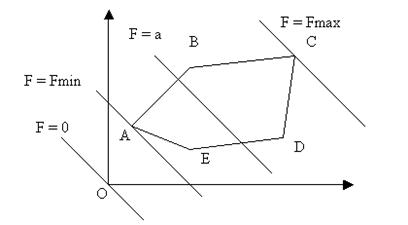
Предположим, точка А – исходное ДБР (допустимое базисное решение). Из чертежа видно, что от А выгодно перейти к В, а потом к С.

Идея последовательного улучшения решения легла в основу универсального метода решения ЗЛП – симплексного метода.

Впервые был предложен амер. ученым Дж. Данцигом в 1949 г., хотя идеи метода были разработаны Л. В. Канторовичем в 1939 году.

Метод используется для компьютерных расчетов.

Для реализации метода необходимо освоить три основных элемента:

§ способ определения первоначального ДБР задачи;

§ правило перехода к лучшему (не худшему) решению;

§ критерий проверки оптимальности найденного решения.

Для использования симплексного метода ЗЛП д.б. приведена к каноническому виду, т.е. система ограничений – в виде уравнений.

Дата добавления: 2014-01-15