Временная форма представления сигнала

ЛЕКЦИЯ 3

Временным представлением сигнала называют такое разложение сигнала u(t), при котором в качестве базисных функций используются единичные импульсные функции – дельта-функции.

Математическое описание такой функции задается соотношением

¥ при t = 0

d(t) = (9)

0 при t ¹ 0

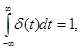
где d(t) – дельта-функция, отличная от нуля в начале координат (при t=0).

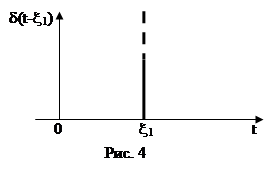Для более общего случая, когда d ¹ 0 в момент времени t = x₁ (рис. 4),

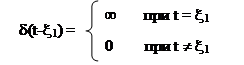(10)

Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени x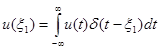₁:

(11)

Равенство (11) справедливо для любого текущего t. Заменив x₁ на t и приняв в качестве переменной интегрирования x, получим

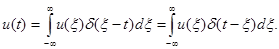(12)

Т.о. функция u(t) выражена в виде совокупности примыкающих друг другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Разложение (12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.

С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянным или меняющимся уровнями.

Обозначив через u_п(t) функцию, равную u(kDt) в точках t= kDt и нулю в остальных точках, запишем

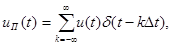(13)

где Dt - период следования импульсов.

Поскольку умножение u(t) на дельта-функцию в момент времени t = kDt соответствует получению отсчета этой функции u_п(kDt) может представлять результат равномерной дискретизации функции u(t).

Дата добавления: 2014-01-15