ЛЕКЦИЯ 4. Спектры непериодических сигналов

Спектры непериодических сигналов.

Любой реальный физический сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы удовлетворяют условиям Дирихле и абсолютно интегрируемы, т.е.

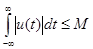(40)

где М – конечная величина.

Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в соответствии с выражением (2) (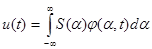). Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, происходящие в спектре периодической последовательности импульсов u₁(t) при увеличении периода их повторения.

В соответствии с (30), которая справедлива для любого значения периода Т, абсолютные значения амплитуд спектральных составляющих в (27) при увеличении периода уменьшаются. Т.к. частоты составляющих спектра кратны основной частоте, то при ее уменьшении линии на спектральной диаграмме сближаются.

Спектральное представление для одиночного импульса u(t) получим как следствие увеличения периода сигнала u₁(t) до бесконечности.

Пару преобразований Фурье для периодической функции u₁(t) запишем в форме (15) и (16)

,

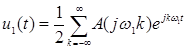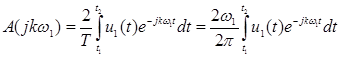
При Т ® ¥ u₁(t) переходит в u(t), частота w₁ уменьшается до dw, а kw₁ превращается в текущую частоту w. Заменяя суммирование интегрированием, находим:

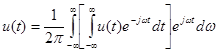
Обозначив интеграл в квадратных скобках S(jw), получим формулы для прямого и обратного преобразования Фурье

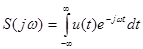(41)

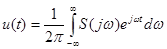(42)

Величину S(jw) называют комплексной спектральной плотностью или спектральной характеристикой.

Она имеет размерность [амплитуда/частота]. На каждой конкретной частоте амплитуда соответствующей составляющей равна нулю. Сравнивая (15) и (42) находим, что бесконечно малому интервалу частоты dw соответствует составляющая с бесконечно малой комплексной амплитудой dA(jw).

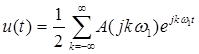(15)

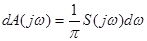(43)

Сравнение выражения (41) для спектральной характеристики функции u(t), заданной на интервале времени t₁ £ t £ t₂, с формулой (17) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, показывает, что они различаются только множителем.

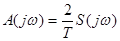(44)

Поэтому по известной спектральной характеристики одиночного импульса легко построить линейчатый спектр их периодической последовательности. Соотношением (44) объясняется и тот факт, что для различных представлений спектральной характеристики имеют место формулы, весьма похожие на (18)... (24).

Как комплексная величина S(jw) имеет вид

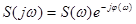(45)

где 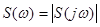называется спектральной плотностью амплитуд или спектром непериодического сигнала.

Т.к. составляющие расположены на всех частотах, то спектр периодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей:

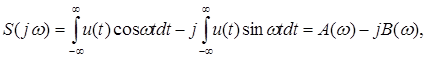
где

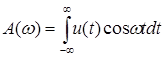(47)

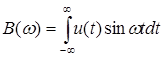(48)

Модуль S(jw) равен

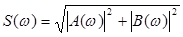(49)

и представляет собой четную функцию частоты.

Фаза S(jw)спектральной характеристики равна

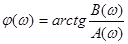(50)

Т.к. из (42) и (43) следует, что А(w) – четная функция частоты, а В(w) – нечетная, то функция j(w) относительно частоты нечетна.

Комплексная форма преобразования Фурье легко приводится к тригонометрической:

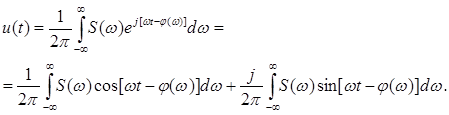
Второй член в связи с нечетностью подынтегрального выражения равен нулю

Окончательно имеем

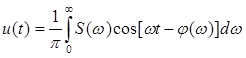(51)

Дата добавления: 2014-01-15