
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Завадостійкість при складних видах модуляції
|
|
|
|
Завадостійке кодування на фізичному рівні
Раніше уже одержано дуже важливий висновок щодо можливого впливу завадостійкого кодування на енергетичні співвідношення в каналах. Цей висновок зводиться до того, що застосування завадостійкого кодування надає певний енергетичний виграш і є еквівалентним збільшенню співвідношення сигнал/завада в
g = (h /)2 / h 2 = R (t +1)
разів. До того ж, виходячи із структури об’єктів завадостійкого кодування та параметрів, зокрема значності застосованих кодів, можна зробити висновок щодо можливостей застосування такого кодування щодо інформаційних об’єктів значного обсягу, тобто переважно на транспортному та мережному рівнях (застосування способів обміну із перезапитом), а також на канальному рівні (застосування способів обміну із завадостійкими корегуючими кодами чи як перший етап застосування способів обміну із перезапитом).
Отже в подальшому повинно йтися про можливості підвищення завадостійкості по відношенню до груп бінарних об’єктів незначного обсягу (сигнали при різних видах багаторівневої модуляції). Для цього спочатку порівняємо завадостійкість при модуляції бінарних сигналів і більш складних видів модуляції. При цьому використаємо геометричне трактування щодо представлення сигналів, коли сигнали відображаються векторами в певному сигнальному просторі, координатні вісі якого визначаються застосованими методами модуляції. Причому, кінці векторів в цьому просторі відображаються у вигляді сигнальних точок, координати яких визначаються значеннями параметрів, що модулюються (наприклад, в системі КАМ – координатами x (t) і у(t)). Сукупність сигнальних точок утворює, так зване, сигнальне сузір’я (signal constellation).
Сигнали при застосуванні АМ можна відобразити як вектор на числовій вісі (0, А), а сигнали із модуляцією двох параметрів можна зобразити у вигляді точок (кінців векторів) на площині. В останньому випадку простір сигналів складають сигнали із дискретними положеннями вершин сумарних векторів ( ). При застосуванні фазової чи амплітудно – фазової модуляції це може трактуватися як амплітуда А та фаза сигналу Q). При застосуванні квадратурно – амплітудної модуляції це може трактуватися як синфазна
). При застосуванні фазової чи амплітудно – фазової модуляції це може трактуватися як амплітуда А та фаза сигналу Q). При застосуванні квадратурно – амплітудної модуляції це може трактуватися як синфазна  та квадратурна
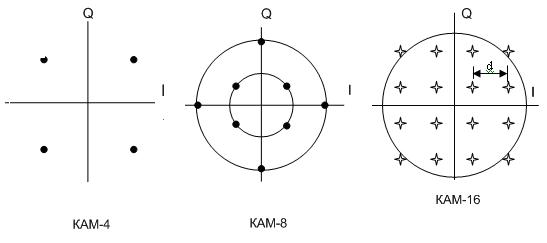
та квадратурна  складові. На рис. 1 показані типові ансамблі сигналів з АМ, ФМ, АФМ і КАМ.
складові. На рис. 1 показані типові ансамблі сигналів з АМ, ФМ, АФМ і КАМ.
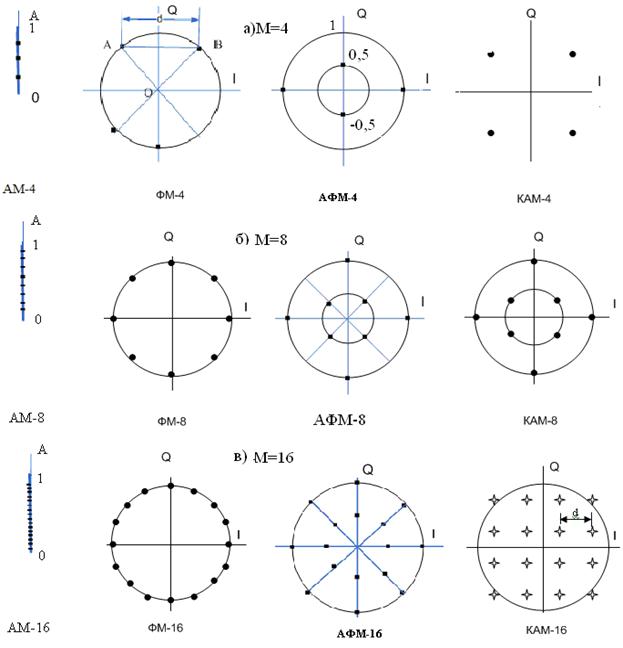
Рис. 1. Ансамблі сигналів АМ, АФМ, ФМ і КАМ при різних кількостях
сигнальних точок М
Виявляється, що при багаторівневих сигналах завадостійкі властивості кодів визначають мінімальні евклідові відстані між сигнальними точками, що виходять при різних способах кодування і різних схемах модуляції.
Нагадаємо, що евклідовою відстанню між двома точками а і b n -координатного (і = 1, 2,…, п) простору називається величина:
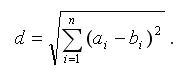
Ці відстані, не в останню чергу, залежать від кількості та порядку розташування сигнальних точок відповідного сузір’я на координатних площинах при двопараметричній, чи на числовій вісі при однопараметричній модуляції. Надалі для можливості порівнювати між собою мінімальні евклідові відстані в залежності лише від виду модуляції будемо вважати, що потужності сигналів, а отже і їх амплітуди (А) є нормованими, тобто однаковими (А = 1).
Неважно визначити, що при однопараметричній багаторівневій амплітудній модуляції і нормованому значенні А = 1 мінімальна відстань дорівнює 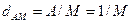 , де: А – величина амплітуди сигналу; М – кількість градацій сигналу на вісі амплітуд, у цьому випадку, – кількість амплітудних дискрет.
, де: А – величина амплітуди сигналу; М – кількість градацій сигналу на вісі амплітуд, у цьому випадку, – кількість амплітудних дискрет.

При ФМ мінімальна відстань між точками визначається, як довжина хорди при центральному куті α = 2π/M та радіусі кола r = А:  , де М –кількість фаз.
, де М –кількість фаз.

Наприклад, при М = 4 (рис. 1 а) у випадку ФМ сигнальні точки розташовані на векторах ОА та ОВ, які рознесені на кут π/2 і відповідають фазам, що можуть дискретно приймати значення 0°, 90°, 180° або 270°. Для визначення мінімальної відстані при ФМ слід розглянути трикутник АОВ. Неважко бачити, що цей трикутник має рівні сторони ОА та ОБ та центральний кут між ними, який дорівнює 2π/ М. Отже, при М = 4 ця величина дорівнює  .
.
Використовуючи аналогічний підхід, можна визначити мінімальні відстані між точками для АФМ із m рівнями модуляції по амплітуді та із кількістю фаз, що дорівнює l, так що  .
.
Неважко показати, що така відстань дорівнює
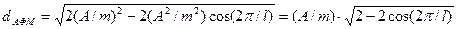 .
.
При тих же умовах (М = 4) у випадку АФМ фази векторів I і Q міняються також дискретно і можуть приймати значення 0° або 180° – для вектора I, і 90° і 270° – для вектора Q. Із рис. 1а видно, що для АФМ мінімальна відстань між сигнальними точками дорівнює  .
.
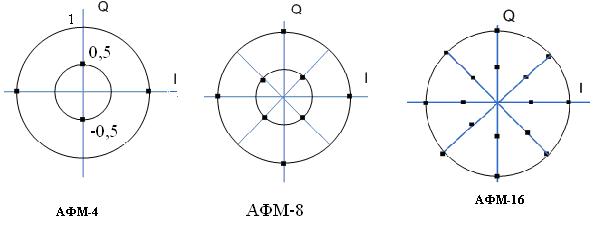
При цьому енергія ФМ сигналів в процесі модуляції не міняється, і вершини сумарного вектора I + Q при переході від одного фазового положення до іншого описують коло (рис. а, б, в). У випадку АФМ та КАМ-16 енергія сигналів дещо змінюється так, що кінці сигнальних векторів АФМ розташовуються на декількох колах із відповідною енергією, а кінці сигнальних векторів при КАМ – у вузлах прямокутних ґрат (рис. 1 в).
Мінімальна відстань d між сусідніми точками сигнального сузір’я в системі КАМ з 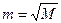 рівнями модуляції по кожному із параметрів (по одній із координат) може бути знайдена (див. рис. 2) як 1/(m –1) частка проекції подвійного значення максимального рівня сигналу на горизонтальну (або ж вертикальну) вісь. Враховуючи те, що при нормованій потужності сигналу проекція максимального рівня сигналу на цю вісь дорівнює
рівнями модуляції по кожному із параметрів (по одній із координат) може бути знайдена (див. рис. 2) як 1/(m –1) частка проекції подвійного значення максимального рівня сигналу на горизонтальну (або ж вертикальну) вісь. Враховуючи те, що при нормованій потужності сигналу проекція максимального рівня сигналу на цю вісь дорівнює  , подвійна проекція дорівнює
, подвійна проекція дорівнює  . Отже, ця мінімальна відстань визначається виразом
. Отже, ця мінімальна відстань визначається виразом 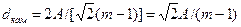 . У цьому випадку мінімальна відстань визначається виразом
. У цьому випадку мінімальна відстань визначається виразом 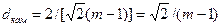 .
.
Звернемо увагу також те, що мінімальні відстані для ФМ і КАМ є рівними  , а також на те, що, як відомо, при рівному числі точок в сигнальному сузір’ї спектри сигналів АФМ і КАМ ідентичні спектру сигналів ФМ.
, а також на те, що, як відомо, при рівному числі точок в сигнальному сузір’ї спектри сигналів АФМ і КАМ ідентичні спектру сигналів ФМ.
Не важко упевнитися, що мінімальні відстані міх сигнальними точками можуть приймати значення згідно із таблицею 1. В таблиці, для одержання порівняльних результатів, прийнято нормоване значення амплітуди А = 1.
Оскільки відстань між сигнальними точками в системі АФМ менше відстані між сигнальними точками в системі ФМ, а відстань між сигнальними точками в системі ФМ, в свою чергу, менше відстані між сигнальними точками в системі КАМ, то можна стверджувати, що при однаковому числі точок і однаковій нормованій потужності сигналу сигнали системи КАМ мають найкращу завадостійкість, ніж сигнали систем ФМ та АФМ.
Таблиця 1. Значення мінімальних відстаней для різних видів модуляції
| Вид модуляції | Вираз для розрахунку 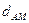 ( (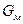 ) )
| Значення 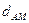
| |||
| М = 4 (m = 2, l = 2) | М = 8 (m = 2, l = 4) | М = 16 (m = 4, l = 4) | М = 32 (m = 4, l = 8) | ||
| АМ | А/М | 0,25 | 0,125 | 0,0625 | 0,03175 |
| АФМ | 
| 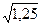
| 0,5 | 0,250 | 0,049 |
| ФМ | 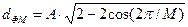
| 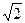
| 0,765 | 0,392 | 0,196 |
| КАМ | 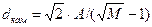
| 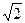
| 0,771 | 0,471 | 0,283 |
| КАМ/ФМ |  , дБ , дБ
| 0,6 | 1,62 | 3,2 |
Дійсно, якщо необхідно здійснити порівняння видів модуляції сигналів, наприклад, КАМ і ФМ, то критерієм в цьому випадку може служити асимптотичний енергетичний виграш, який можна визначити відомою формулою:
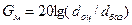 ,
,
де: dбаз – мінімальна евклідова відстань між різними послідовностями в базовій системі, а dоц – мінімальна евклідова відстань між різними послідовностями в системі, яка оцінюється.
Зокрема, якщо базовою системою є система із ФМ, а системою, яка оцінюється є система із КАМ, то:
 ,
,
де dКАМ – мінімальна евклідова відстань між різними послідовностями в системі КАМ, а dФМ – в системі ФМ.
Як приклад, для наведених вище параметрів КАМ і ФМ при збільшенні кількості фаз М при ФМ, чи збільшенні кількості амплітудних рівнів m при КАМ можна получити:
при М = 16, m = 4:  дБ,
дБ,
при М = 32, m = 6: 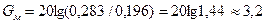 дБ,
дБ,
що свідчить про збільшення відносної завадостійкості КАМ щодо ФМ.
Залежності Рвикр (h) для деяких видів модуляції приведені на рис. 2. Видно, що сигнали КАМ, порівняно із ФМ, при однаковій кратності мають кращу завадостійкістю. Це пояснюється більш рівномірним розташуванням сигнальних точок по всьому сигнальному простору, що забезпечує великі значення мінімальної відстані.
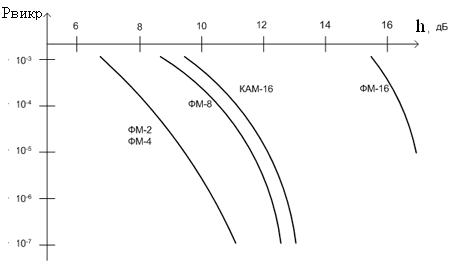
Рис. 2. Залежність Рвикр для деяких видів модуляції
З іншого боку, якщо порівняти між собою системи із ФМ при М = 16 та М = 32, і системи із КАМ при m = 4 та при m = 6, то:
при ФМ із М = 16, М = 32: 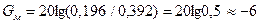 дБ,
дБ,
при КАМ із m = 4, m = 6:  дБ.
дБ.
Одержані результати (див. рис. 2) свідчать про те, що збільшення кількості фаз М при ФМ, чи збільшення кількості амплітудних рівнів m і фаз l при АФМ і КАМ призводять до збільшення пропускної спроможності каналів і, водночас, до зменшення абсолютної завадостійкості обох систем за рахунок зменшення значень мінімальних відстаней між сигнальними точками при відповідному збільшенні їх кількості.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 986; Нарушение авторских прав?; Мы поможем в написании вашей работы!