Аксиоматическое построение теории вероятностей

В случае с геометрическими вероятностями пространство элементарных исходов не конечно и даже не счетно, а значит невозможно применять классическую формулу для подсчета вероятностей. Проблема определения вероятностей, когда классическая формула неприменима, была решена Андреем Николаевичем Колмогоровым, который в 1929 году сформулировал аксиоматику теории вероятностей. Работы Колмогорова в области теории вероятностей считаются самым крупным вкладом в математическую науку в ХХ столетии. В чем эта аксиоматика состоит?

Пусть пространство элементарных событий 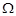есть произвольное множество, и пусть - некоторая система его подмножеств.

называется алгеброй, если

1) ;

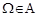2) для любых множеств B, C принадлежащих , так же принадлежит .

3) если 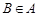, то и .

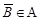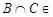
Из этих свойств также следует, что для любых множеств , принадлежащих , их пересечение , (т.к.).

Таким образом, алгебра – это класс множеств, замкнутый относительно операций дополнения, объединения и пересечения.

Замечание. Алгебра может быть замкнута не только относительно конечного числа этих операций, но также их счетного числа. В этом случае она называется 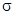- алгеброй.

Если задано множество W и какая-нибудь алгебра его подмножеств , то говорят, что задано измеримое пространство (W, ).

Пример 7. В примере 4 предыдущего параграфа пространство W состоит из точек отрезка [ А, В ]. Совокупность множеств { W, , [ C, В ], [ А, C)} образует алгебру . ¨

Для того чтобы формализовать какую-либо вероятностную задачу, надо соответствующему эксперименту приписать измеримое пространство (W, ).
W означает множество элементарных исходов эксперимента, алгебра выделяет класс событий. Все остальные подмножества W, которые не вошли в алгебру , cобытиями в данном эксперименте не являются.

Пусть (W, ) - измеримое пространство. Вероятностью на измеримом пространстве (W, ) называется числовая функция Р, определенная на множествах из и удовлетворяющая трем аксиомам:

1) для любого множества :;

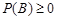2) ;

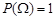3) для любых двух событий В и С, принадлежащих алгебре и таких, что : .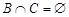

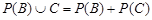Замечание. Если является 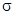- алгеброй, третье утверждение должно выполняться не только для конечного, но также для любого счетного объединения ее подмножеств. В этом случае третья аксиома называется аксиомой счетной аддитивности.

Тройка (W, , 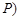называется вероятностным пространством.

Пример 8. В примере 7 вероятность любого события из алгебры положим равной длине соответствующего промежутка, деленной на длину отрезка [ А, В ]. Все аксиомы вероятности будут выполнены.¨

Дата добавления: 2014-01-15