Лекция 8. Cлучайные величины X и Y называются независимыми, если функция распределения cлучайного вектора (X, Y) равняется произведению функций распределения компонент

§ 4. ЗАВИСИМОСТЬ И КОВАРИАЦИЯ.

Cлучайные величины X и Y называются независимыми, если функция распределения cлучайного вектора (X, Y) равняется произведению функций распределения компонент X и Y:

.

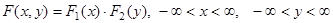Утверждение 3. Непрерывные случайные величины независимы тогда и только тогда, когда плотность случайного вектора (X, Y) равняется произведению плотностей компонент X и Y: .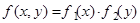

Для доказательства необходимости продифференцируем по x и y обе части равенства из определения независимых случайных величин. Для доказательства достаточности возьмем интегралы от обеих частей равенства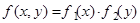по области {(-¥, x), (-¥, y)} §

Утверждение 4. Дискретные случайные величины независимы тогда и только тогда, когда 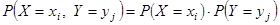для любых пар значений 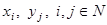, случайных величин X и Y.

Доказательство.

§

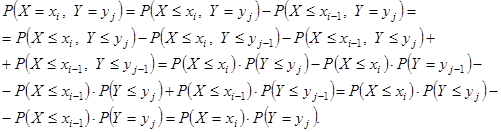Пример 6. В примере 1 § 1 плотность случайного вектора (X,Y) 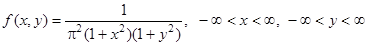, а плотности компонент .

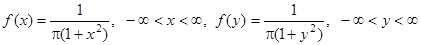Следовательно, cлучайные величины X и Y независимы. ¨

Утверждение 5. Для независимых случайных величин X и Y ковариация равна 0.

Доказательство. Из утверждений 2 и 3 следует, что для независимых случайных величин X и Y M (XY) = M (X) × M (Y), если M (X) и M (Y) существуют.

Для непрерывных случайных величин это так, поскольку

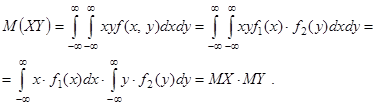
Для дискретных случайных величин

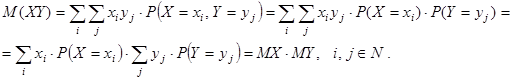
Отсюда, сov(X, Y) = M (XY) – M (X) M (Y) = 0. §

Замечание. M (XY) = M (X) × M (Y) также, если одна из независимых случайных величин непрерывного, а другая дискретного типа.

Таким образом, ненулевая ковариация - это признак наличия зависимости между случайными величинами.

Утверждение 6. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих случайных величин.

Доказательство сразу следует из формулы для дисперсии суммы случайных величин. §

§ 5. KОЭФФИЦИЕНТ КОРРЕЛЯЦИИ И ЕГО СВОЙСТВА.

Если ковариация случайных величин X и Y (cov(X, Y) = M ((X – MX)(Y –
– MY))) невелика, то это не всегда является следствием слабой зависимости между ними, а может просто указывать на то, что случайные величины мало отклоняются от своего математического ожидания. Поэтому для характеристики связи случайных величин рассматривают коэффициент корреляции:

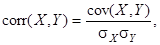
где 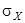и 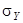- средние квадратические отклонения случайных величин X и Y.

Случайные величины, для которых ковариация, а значит и коэффициент корреляции равны нулю, называются некоррелированными.

Из независимости вытекает некоррелированность, обратное неверно. Коэффициент корреляции может оказаться равным нулю, когда одна случайная величина является функцией от другой.

Пример 7. Пусть случайные случайные U и V имеют одинаковые распределения и X = U + V, Y = U – V. Тогда M (XY)= M (X²) – M (Y ²) = 0 и
M (Y) = 0. Cледовательно, cov(X, Y) = M (XY) – M (X)(Y) = 0, и поэтому corr(X, Y) = 0. Например, X и Y могут быть соответственно суммой и разностью очков, выпавших на двух костях. Тогда величины X и Y либо обе четны, либо обе нечетны и, cледовательно, зависимы. ¨

Пример 8. Из некоррелированности случайных величин, подчиненных двумерному нормальному закону, вытекает их независимость. Действительно, параметр r двумерного нормального распределения совпадает с коэффициентом корреляции, и следовательно плотность распределения

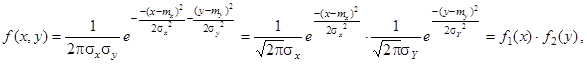где 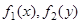- плотности компонент Х и Y.

Таким образом, для компонент X и Y нормально распределенного случайного вектора свойства некоррелированности и независимости совпадают.¨

Коэффициент корреляции обладает следующими свойствами:

Утверждение 7. corr (X, Y) £ 1.

Доказательство. Введем случайную величину .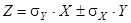

, DZ ³ 0. Cледовательно, ; ; ; ; .§

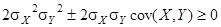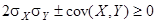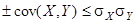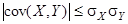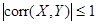Утверждение 8. Если X и Y cвязаны точной линейной функциональной зависимостью Y = aX + b, то

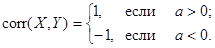
Доказательство:

; §

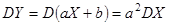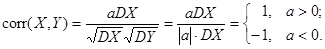Таким образом, коэффициент корреляции является характеристикой линейной зависимости между случайными величинами.

Пример 9. Вернемся к плотности двумерного нормального закона. Уравнения эллипсов рассеивания двумерной нормальной плотности

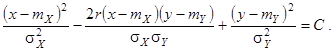
Если коэффициент корреляции r > 0, главные оси эллипсов расположены под некоторым углом a к координатным осям (из аналитической геометрии известно, что 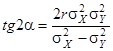). Происходит как бы “намагничивание” двумерного случайного вектора вдоль одной из главных осей y = kx + b, т.е. линейная составляющая присутствует в функциональной зависимости между X и Y. Если же коэффициент корреляции r = 0, уравнения эллипсов

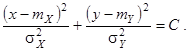
Главные оси рассеивания параллельны осям координат у = 0, x = 0. Линейной зависимости между компонентами X и Y нет. ¨

Дата добавления: 2014-01-15