Общие принципы преобразования

Выше было показано, что используя степенной полином (2.1) и выбирая различные значения основания P, можно создавать разнообразные системы счисления.

В процессе обмена информацией, ее хранения и организации работ функциональных устройств и компонентов компьютера, приходится преобразовывать информацию из одной системы счисления в другую и обратно, для повышения эффективности вычислений и оптимального использования компонентов компьютера.

Так, например, числа традиционной десятичной системы счисления переводятся в коды двоичной, восьмеричной, шестнадцатеричной, двоично-кодированной десятичной системы счисления и обратно. При этом широко используется простой способ последовательного деления числа и его частного на основание системы, в которую требуется перевести искомое число. Деление производится до тех пор, пока частное не будет меньше основания системы.

Пример. Преобразовать десятичное число 115₍₁₀₎ в двоичное, восьмеричное, шестнадцатеричное.

Стрелками обозначены направления записи искомых чисел:

115₍₁₀₎ = 1110011₍₂₎ = 163₍₈₎ = 73₍₁₆₎

Для проверки правильности вычислений производится обратный перевод чисел в десятичную систему счисления, используя выражения (2.1) (2.3):

а) 1110011₍₂₎ = 1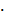2⁶ + 1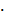2⁵ + 1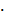2⁴ + 0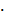2³ + 0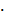2² + 1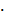2¹ + 1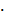2⁰ =

= 64 + 32 + 16 + 0 + 0 + 2 + 1 = 115₍₁₀₎

б) 163_{(8) ­} = 1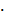8² + 6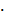8¹ + 3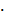8⁰ = 64 + 48 + 3 = 115₍₁₀₎

в) 73₍₁₆₎ = 7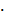16¹ + 3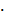16⁰ = 115₍₁₀₎

Для преобразования правильной дроби из системы счисления с основанием P₁ в систему с основанием P₂ необходимо последовательно умножать дробь и последующие дробные части, полученных произведений, на основание P₂до получения во всех разрядах нулей или требуемой точности. Целые числа этих произведений, записанные по ходу выполнения действий (с лева направо), и будут представлять число в новой системе счисления.

Пример. Десятичное число 0,768₍₁₀₎ преобразовать в двоичное, восьмеричное с точностью , .

а)

Искомое число:

0,768₍₁₀₎ = 0,1100₍₂₎

Возможная наибольшая ошибка будет .

б)

Искомое число:

0,768₍₁₀₎ = 0,61115₍₈₎

Возможная наибольшая ошибка будет .

Более универсальным способом перевода чисел из одной системы счисления в другую можно считать способ использования степенного полинома (2.1). Т.е. число в системе счисления 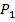представляется степенным полиномом, но уже в другой системе счисления :

(2.4)

Решение задачи сводиться к определению степени n полинома и коэффициентов

Рассмотренные преобразования подчиняются общему алгоритму, приведенному ниже.

Пример. Преобразовать десятичное число в двоичное, восьмеричное, шестнадцатеричное с точностью до

Записывается полином (2.4) по убывающим степеням для соответствующего основания и допустимой ошибки.

1).

Определяется степень полинома n из (2.5)

Максимальное значение n = 6, которое не нарушает это неравенство

Принимаем и далее записывается полином с учетом алгоритма:

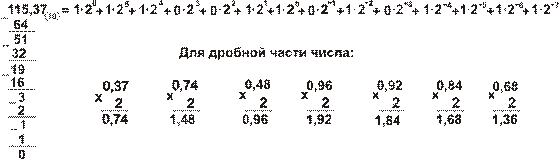
Искомое десятичное число преобразовано в двоичную форму:

2).

Дата добавления: 2014-01-15