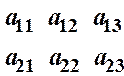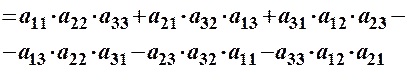Визначники, їх властивості

Нехай 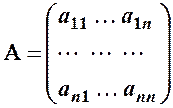– ­­квадратна матриця -го порядку.

Означення. Визначником квадратної матриці -го порядку (або просто визначником -го порядку) називається число, яке обчислюється за певним правилом, і позначається:

.

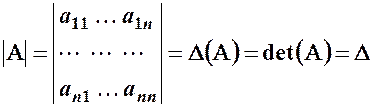Так, наприклад, визначник 1–го порядку: ,

Тобто, визначник квадратної матриці 1–го порядку дорівнює елементу матриці (визначника).

Наприклад: , .

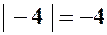Для знаходження правила обчислення визначників вищих порядків уведемо поняття мінора та алгебраїчного доповнення елемента визначника.

Нехай 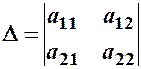– визначник 2–го порядку.

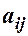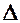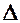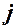Означення. Мінором елемента визначника називається визначник, який отримується із викреслюванням (вилученням) -го рядка та -го стовпця.

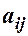Означення. Алгебраїчним доповненням елемента визначника 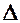називається його мінор, взятий зі знаком „+” або „–”:

.

Для визначника 2–го порядку:

;;

; .

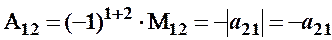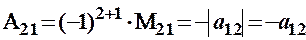Теорема Лапласа (про розклад визначника). Визначник дорівнює сумі добутків елементів деякого одного рядка (або деякого одного стовпця) визначника на відповідні їм алгебраїчні доповнення.

Так, для визначника 2–го порядку, за теоремою Лапласа:

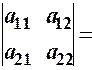(розклад за 1–им рядком) = .

Відзначимо, що теорема дозволяє звести обчислення визначника 2–го порядку до знаходження визначників 1–го порядку (в загальному випадку, обчислення визначника -го порядку зводиться до обчислення визначників -го порядку).

Зауваження. На практиці визначник 2–го порядку зручніше обчислювати за таким правилом: визначник дорівнює добутку елементів головної діагоналі мінус добуток елементів побічної діагоналі.

Наприклад:

.

Нехай 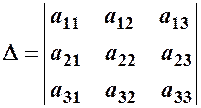- визначник 3–го порядку.

За теоремою Лапласа запишемо розклад визначника, наприклад, за елементами 1–го сповпця:

.

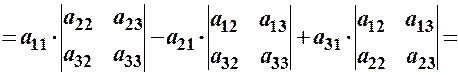
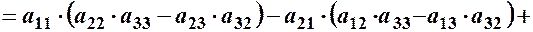
Зауваження. На практиці визначник 3–го порядку зручніше знаходити за так званим „правилом Саріуса”:

1) припишемо під визначником 1–ий та 2–ий рядки:

+ + ∆=

– –

–

+

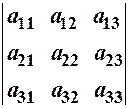
2) зі знаком „+” беремо добутки елементів головної діагоналі та трійок елементів, паралельних цій діагоналі; зі знаком „–” беремо добутки елементів побічної діагоналі та трійок елементів, паралельних цій діагоналі.

–

+

Наприклад:

+ +	– –

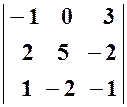
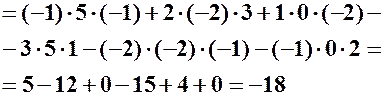
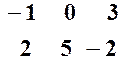
Зауваження. Для визначників 4-uj та більш високих порядків немає зручних правил для їх обчислення, тому доводиться користуватись теоремою Лапласа. При цьому, очевидно, для скорочення обчислень краще розкладати визначник за рядком або стовпцем, у яких є нульові елементи.

Дата добавления: 2014-01-15