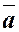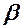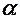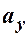КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектором називається напрямлений відрізок прямої
|
|
|
|
Основні означення
Елементи векторної алгебри
Величини бувають скалярні та векторні.
Величина називається скалярною, якщо вона повністю визначається своїм числовим значенням в обраній системі одиниць вимірювання.
Наприклад, довжина відрізка, температура, площа, час, об’єм, робота тощо.
Величина називається векторною, якщо вона визначається не тільки числовим значенням, але і напрямком.
Наприклад, швидкість, сила, прискорення.
Для характеристики таких величин уводять поняття вектора. Розділ математики, в якому вивчаються дії над векторами, називається векторною алгеброю. Векторна алгебра широко використовується у сучасній аналітичній геометрії.

|
|
 – початок, а точка
– початок, а точка  – кінець вектора, то це позначається
– кінець вектора, то це позначається 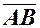 або
або 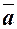 .
.
 |
Довжина цього відрізка називається довжиною або модулем вектора і позначається 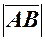 або
або 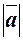 .
.
Вектор, початок якого співпадає з кінцем, тобто модуль якого дорівнює нулю, називається нульовим і позначається 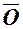 . Очевидно, напрямок нульового вектора довільний.
. Очевидно, напрямок нульового вектора довільний.
Вектори, які лежать на паралельних прямих або на одній і тій самій прямій, називаються колінеарними.
  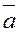
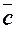
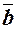 
| 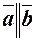 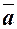 і і 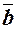 колінеарні, співнапрямлені. колінеарні, співнапрямлені.
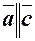 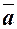 і і 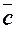 колінеарні, протилежно напрямлені. колінеарні, протилежно напрямлені.
|
Два вектори називаються рівними 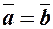 , якщо вони колінеарні, мають однаковий напрямок і однакову довжину.
, якщо вони колінеарні, мають однаковий напрямок і однакову довжину.
З останнього означення випливає, що при паралельному перенесенні ми отримуємо вектор, рівний даному.
В алгебраїчній формі вектор можна задати його проекціями на вісі координат, тобто 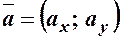 .
.
Якщо помістити початок вектора в точку 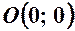 (це завжди можна зробити паралельним перенесенням), то координати його кінця будуть дорівнювати проекціям вектора на вісі координат.
(це завжди можна зробити паралельним перенесенням), то координати його кінця будуть дорівнювати проекціям вектора на вісі координат.
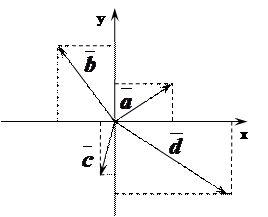
  
| Приклад.
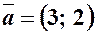 ; ; 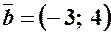 ; ;
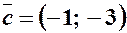 ; ; 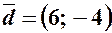 .
Таким чином, між векторами на площині та упорядкованими парами дійсних чисел встановлено взаємооднозначну відповідність. .
Таким чином, між векторами на площині та упорядкованими парами дійсних чисел встановлено взаємооднозначну відповідність.
|
Напрямок вектора визначається за допомогою напрямних косинусів, якими є косинуси кутів, утворених вектором з осями координат.
|
 
| Напрямні косинуси обчислюються за формулами:
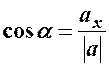 ; ; 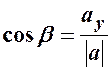 .
З попереднього прикладу для вектора .
З попереднього прикладу для вектора 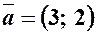 : :
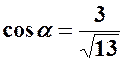 ; ; 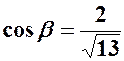 . .
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1247; Нарушение авторских прав?; Мы поможем в написании вашей работы!