Стандартне відхилення

Статистичні моделі прийняття маркетингових рішень з урахуванням фактора невизначеності.

В управлінській діяльності часто виникають ситуації, за яких доводиться приймати рішення, виходячи з недостатньо чітко визначених умов і оперуючи не завжди надійною інформацією. У таких випадках виникає потреба в оцінюванні ймовірності досягнення тих чи інших результатів. Наприклад, якщо буде прийняте рішення А, то ймовірність досягнення додаткового прибутку у розмірі 10 % становитиме 95 %, а за рішення В вона зменшиться до 65 %.

Існує три основних методи, що дають змогу приймати рішення з урахуванням фактора невизначеності та підтримуються Excel: стандартні відхилення, довірчі інтервали і множинний регресійний аналіз.

Стандартне (середнє квадратичне) відхилення — ступінь відхилення усіх значень ознаки від свого середнього показника — є одним із найважливіших методів, що допомагають визначити, наскільки змінюється певна величина: чим більше стандартне відхилення, тим ширший діапазон змін значень цієї величини.

Припустимо, що слід проаналізувати ефективність діяльності торгових агентів і продавців. Варто наголосити, що для більшості підприємств цей показник є найвагомішим серед тих, що впливають на збут. Під діяльністю торгових агентів і продавців розуміється робота, що проводиться ними безпосередньо з потенційними покупцями: за прилавком магазину, під час відвідування клієнтів за місцем проживання або прийому попередніх замовлень телефоном. Якщо такі працівники зацікавлені у результатах своєї діяльності, добре знають товар, який продають, і мають відповідний комерційний хист, то їх внесок в успіх фірми можна вважати вирішальним.

Природно розпочати аналіз з визначення середньої суми комісійних, яку фірма сплачує цій категорії своїх працівників. Функція Excel, яка розраховує середні показники, має назву СРЗНАЧ. Вона підсумовує значення клітин вказаного діапазону і ділить цю суму на кількість його клітин. Проте одна ця цифра ще не дає змоги оцінити роботу торгових агентів, оскільки середня величина — це узагальнена характеристика тієї сукупності, що вивчається. Вона не показує побудови сукупності, яка є дуже суттєвою для пізнання останньої. Окремі значення можуть зосереджуватися біля середньої величини (тоді вона добре представляє всю сукупність) або значно відхилятися від неї (погано представляє сукупність). Показником надійності середньої величини є стандартне (середньоквадратичне) відхилення: близько двох третин окремих елементів сукупності знаходяться на одне стандартне відхилення нижче або вище середнього показника.

Так, якщо за середньорічного заробітку 1440 грн стандартне відхилення дорівнює 107 грн, то це означає, що заробіток двох третин торгових агентів становить (1440 ± 107) грн, звідки випливає, що ефективність їхньої роботи практично збігається. Якщо ж заробіток двох третин торгових агентів становить, наприклад, (1440 ± 645) грн, то це означає, що середнє значення (1440 грн) погано представляє сукупність, а отже, значна кількість торгових агентів працює по-різному і є сенс у тому, щоб з’ясувати причини такого становища.

Для підвищення наочності такого аналізу використовуються гістограми (рис. 2.3.1) і точкові діаграми (рис. 2.3.2).

На горизонтальній осі рис. 2.3.1 відкладено різні значення комісійних, на вертикальній — результати спостережень за кожною категорією комісійних (кількість попадань у різні категорії виплат, кожна з яких відрізняється від попередньої на 200 грн). Слід звернути увагу на те, що за меншого значення стандартного відхилення ці результати мають менший розподіл зліва направо, ніж за більшого.

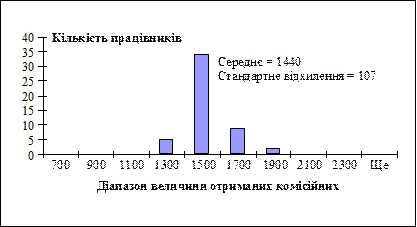
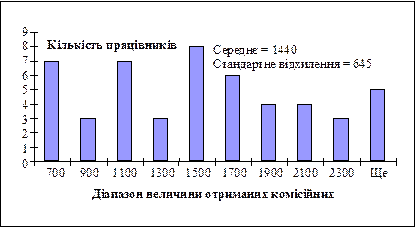
Рис. 2.3.1. Гістограма для різних значень стандартного відхилення

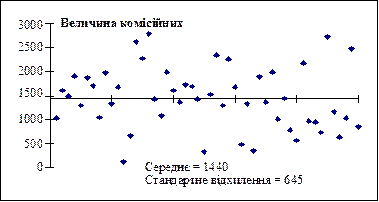
Рис. 2.3.2. Точкова діаграма за різних значень
стандартного відхилення

На рис. 2.3.2 числові значення комісійних відображено на вертикальній осі, а порядковий номер спостереження — на горизонтальній. На верхній діаграмі всі значення близькі до середнього (незначне стандартне відхилення), на нижній спостерігається значне варіювання значень порівняно із середнім. Наведені діаграми показують, що знання середнього значення вибірки ще не є достатнім для прийняття рішення. Якщо ж відомі і середнє значення і стандартне відхилення, то це дає змогу досить чітко уявити, як значення згруповані біля середнього.

У разі суцільного обстеження, тобто коли до уваги беруться дані щодо кожного об’єкта сукупності, формула для обчислення стандартного відхилення має такий вигляд:

,

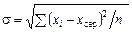де å(х_і – х _сер)² — сума квадратів усіх відхилень окремих значень від їх середньої величини; n — кількість результатів спостережень.

На практиці до суцільного обстеження вдаються рідко. Найчастіше з усієї сукупності випадково відбирається обмежена кількість об’єктів для подальшого дослідження. Якщо в цьому разі для обчислення стандартного відхилення використати наведену вище формулу, то це призведе до систематичних похибок і даватиме зміщене (занижене) значення стандартного відхилення. Для виправлення значення вибіркового стандартного відхилення слід застосовувати формулу:

.

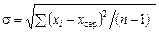Відповідно до цього в Excel є дві функції для обчислення стандартного відхилення: СТАНДОТКЛОНП() і СТАНДОТКЛОН().

Функція СТАНДОТКЛОНП() використовується для обчислення стандартного відхилення за суцільного обстеження, а СТАНДОТКЛОН() — для обчислення стандартного відхилення за вибіркового обстеження. Буква П (у кінці назви першої функції) є мнемонікою слова популяція (генеральна сукупність).

Якщо, наприклад, є 30 результатів вибіркових спостережень, значення яких заведено у клітини В5:В34 робочого аркуша, то для отримання стандартного відхилення всіх цих результатів треба використати формулу

= СТАНДОТКЛОН(В5:В34).

Слід бути вельми обережним у разі використання функцій СТАНДОТКЛОНП() і СТАНДОТКЛОН() для оброблення даних, значення яких або дуже великі (наприклад, 10⁵ і більше), або дуже малі (наприклад, 10^–5 чи менші), оскільки внаслідок впливу піднесення у квадрат різниці результатів спостережень та їх середнього значення будь-яка програма (а не тільки Excel) при округленні може видати похибку. Якщо необхідно працювати з такими даними, можна спробувати перед використанням значень цих функцій змінити масштаб чисел.

Крім стандартного відхилення, для характеристики відхи­лень значень ознаки сукупності від свого середнього значення можна користуватися дисперсією, що дорівнює s². Якщо стан­дартне відхилення можна подати як відстань, то дисперсію — як площину.

В Excel для обчислення дисперсії за суцільного обстеження застосовується функція ДИСПР(), а за вибіркового — ДИСП().

Дата добавления: 2014-01-11