Регресійно-кореляційний аналіз

Регресійний і кореляційний аналіз — дуже ефективні методи, які дають змогу аналізувати значні обсяги інформації з метою дослідження ймовірного взаємозв’язку двох чи більше змінних. У регресійному аналізі розглядається зв’язок між однією змінною, названою залежною змінною, або ознакою, і кількома іншими, названими незалежними змінними. Цей зв’язок подається з допомогою математичної моделі, тобто рівняння, яке зв’язує залежну змінну (y) з незалежними (x) з урахуванням множини відповідних припущень. Оскільки метою регресійного аналізу є виявлення впливу змінних х на значення змінної у, останню ще називають відгуком, або результативним фактором, а змінні х — факторами, що впливають на відгук. Регресійний аналіз використовується з двох причин. По-перше, тому що опис залежності між змінними допомагає встановити наявність можливого причинного зв’язку. По-друге, отримання аналітичної залежності між змінними дає змогу передбачати майбутні значення залежної змінної за значенням незалежних змінних.

За аналізу соціально-економічних процесів регресія застосовується водночас з кореляцією. З допомогою регресії визначаються аналітичні залежності між змінними, а через кореляційний аналіз — сила зв’язку між факторами та відгуком. Саме тому, що основні статистичні проблеми регресійного аналізу вирішуються аналізом кореляцій, методи регресійного та кореляційного аналізу тісно зв’язані між собою.

Математичний апарат кореляційно-регресійного аналізу. Ко­реляційно-регресійний аналіз складається з таких основних етапів: побудова системи факторів, які найсуттєвіше впливають на результативну ознаку; розроблення моделі, яка відбиває загальний зміст взаємозв’язків, що вивчаються, та кількісне оцінювання її параметрів; перевірка якості моделі; оцінювання впливу окремих факторів.

На першому етапі здійснюється відбір факторів, які найсуттєвіше впливають на результатну ознаку. Він проводиться, перш за все, виходячи із змістовного аналізу. Для отримання надійних оцінок у модель не слід включати забагато факторів, їх кількість має бути не більше однієї третини обсягу аналізованих даних. Але оскільки на початковому етапі розроблення моделі у дослідника немає однозначної відповіді на питання щодо набору суттєвих факторів, то у разі використання EОМ відбір факторів звичайно здійснюється безпосередньо в процесі створення моделі за методом послідовної регресії. Суть цього методу полягає у послідовному включенні додаткових факторів у модель та оцінюванні впливу доданого фактора. Використовується також підхід, за якого на фактори, включені у попередній склад моделі, не накладаються особливі обмеження і лише на наступних стадіях проводиться їх оцінювання та часткове відсіювання.

Другий етап починається з розроблення моделі, яка відбиває загальний зміст аналізованих взаємозв’язків. Регресійна модель — це рівняння (або система рівнянь), що показує, які фактори, на думку до­слідника, мають бути залучені до взаємозв’язків, котрі підлягають аналізу. Регресійне рівняння дає також уявлення про форму зв’язку.

Регресія називається парною, якщо вона відбиває залежність між результатною та однією факторною ознаками. Методологія парної кореляції — найбільш розроблена в теорії статистики. Вона є фундаментом для вивчення та застосування інших методів аналізу кореляційного зв’язку.

Регресія називається множинною, якщо вона відбиває залежність результатної ознаки від декількох факторів.

Якщо залежності є лінійними відносно параметрів (але не обов’язково лінійною відносно незалежних змінних), то регресія називається лінійною. В протилежному випадку регресію називають нелінійною.

Під простою регресійною моделлю розуміють парну регресію. У цьому разі статистичний підхід до побудови функціональної залежності у від х базується на припущенні, що є вибірка парних спостережень (х ₁, у ₁), (х ₂, у ₂), …, (х_n, у_n) з деякої популяції. Пару значень (х_і, у_і) часто називають результатом одного вимірювання, а n — кількістю вимірювань.

Для побудови реальної регресійної моделі може використовуватися численна кількість рівнянь. Наприклад, взаємозв’язок частки ринку та відмінностей у ціні можна подати так:

.

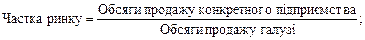
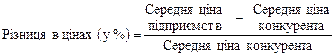Кожну з цих змінних можна подати в декілька способів, використовуючи їх зв’язки з певними факторами:

Залежна змінна (результатна ознака)	Незалежна змінна (фактор)
Обсяги продажу в натуральних одиницях	Середня ціна підприємства
Обсяги продажу в гривнях	Різниця в ціні за одиницю товару
Кількість сімей, що користуються товаром	Середня кількість продукту, куплена сім’єю за місяць

Вибір способів подання зв’язків між змінними визначає дані, які треба зібрати для побудови моделі.

Наступний крок після вибору змінних і способу їх подання –визначення форми рівняння регресії. Тут може стати у пригоді графічне зображення точок (х ₁, у ₁), (х ₂, у ₂), …, (х_n, у_n) на площині ху, назване діаграмою розсіяння (рис. 2.3.3).

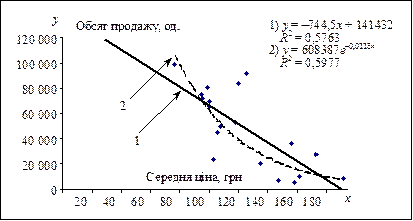
Рис. 2.3.3. Лінії еластичності попиту

Діаграма показує, що зі зростанням ціни частка ринку підприємства дійсно має тенденцію до зменшення. Але яка загальна форма взаємозв’язку? На рисунку цей взаємозв’язок має вигляд прямоліній­ного (лінія 1) та криволінійного (лінія 2) рівняння. Вибір потрібного виду рівняння регресії залежить від знання проблеми та досвіду.

В основу виявлення і встановлення аналітичної форми зв’язку покладено використання певних математичних функцій — ліній-
ної, логарифмічної, степеневої, експоненційної, поліномінальної та деяких інших. У разі парної кореляції ці функції записуються так:

лінійна y = mx + b;

логарифмічна y = mln (x) + b;

степенева y = bx^m;

експоненційна y = bе^mx;

поліномінальна y = m ₆ x ⁶ + m ₅ x ⁵ + … + b.

Практично для обчислення параметрів функцій застосовуються спеціальні комп’ютерні програми, серед яких найбільші можливості для тлумачення результатів користувачеві надають програми лінійного регресійного аналізу. Тому більшість аналітиків віддають перевагу саме йому. Але оскільки лінійні рівняння концептуально являють собою найпростіший тип взаємозв’язку, то його використання потребує особливої остороги.

Для наведеного вище прикладу проста лінійна регресійна модель може бути подана так:

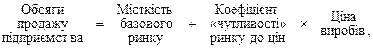
або

y = b + m₁x₁,

де m ₁ < 0.

Відомо, що на частку ринку, яка зайнята товаром, впливають, крім ціни, й інші фактори. А оскільки майже всі проблеми в маркетингу включають у себе кілька різних факторів, то у більшості випадків слід застосовувати моделі множинної регресії. Концепції і методи, використовувані у множинному регресійному аналізі, практично ті самі, що й у простому, але з деякими модифікаціями та доповненнями, пов’язаними з вивченням кількох факторів одночасно. Створення моделі множинної регресії пов’язане також із додатковими труднощами. Перш за все, неможливо дослідити взаємоз’язки з допомогою діаграми розсіяння. Її, звичайно, можна використовувати для відображення взаємозв’язку результативної ознаки й кожного із незалежних факторів по черзі. Але не слід забувати, що отримана в такий спосіб інформація має обмежене значення, оскільки незалежні змінні часто впливають одна на одну так само, як і на результативну ознаку.

У розглядуваному прикладі природно припустити, що на обсяги продажу, крім цін, впливають й витрати на рекламу та дохід споживачів. Отже, наведене вище лінійне рівняння перетворюється на таке:

y = b + m₁x₁+ m₂x₂+ m₃x₃,

де x ₂ — витрати на рекламу;

x ₃ — дохід споживачів.

У разі використання степеневої функції матимемо таку модель:

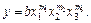
Очевидно, що останнє рівняння є складнішим. Наприклад, вплив на обсяги продажу зміни ціни на 1 грн буде різним залежно від значень інших незалежних факторів. Проте це рівняння є гарним прикладом нелінійного рівняння, яке легко трансформувати у лінійну форму:

log (y) = log (b) + m₁log (x₁) + m₂log (x₂) + m₃log (x₃).

Дані, що збираються для проведення регресійного аналізу, звичайно являють собою «історичні» відомості, тобто цифри, що показують значення кожного із факторів у кожному з попередніх періодів часу або географічних районів. Вони використовуються для отримання оцінок коефіцієнтів регресії та визначення ступеня відповідності моделі дійсним змінам результативної ознаки. Для досягнення цих цілей можна застосовувати різні методи, але найуніверсальнішим і найчастіше використовуваним є метод найменших квадратів. Оцінки за методом найменших квадратів — це ті величини коефіцієнтів регресійного рівняння, які мінімізують суму квадратів відхилень дійсно спостережуваних значень резуль­татної ознаки (у_і) від тих значень, що отримуються з рівняння у (х_і):

å (у_і – у(х_і))² = min.

Метод найменших квадратів дає змогу мінімізувати дисперсію оцінок, а отже, й ступінь невизначеності, пов’язаний з оцінками. У цьому разі дисперсія фактичних значень результативної ознаки від обчислених за рівнянням визначається як

s² = SS_зал /N,

де SS _зал = å(у_i – y (х_і))² — сума квадратів рівнів залишкової компоненти;

N — кількість спостережень.

Для правильного використання результатів, отримуваних на «виході» регресійного аналізу, слід розумітися на суті цих даних і проблемах, пов’язаних з їх тлумаченням. Стосовно аналізу частки ринку підприємства як функції від ціни виробів з допомогою простої лінійної моделі параметри регресії можуть тлумачитися так:

¾ незмінна b — це відрізок на осі координат. Він показує, в якому місці лінія тренда перетинає вісь у (вертикальну вісь). У даному прикладі це значення місткості ринку товару. Проте таке тлумачення не завжди можливе, оскільки результат може являти собою оцінку впливу факторів, не включених в аналіз;

¾ коефіцієнт m рівняння називається коефіцієнтом регресії. Він є мірою нахилу лінії регресії: чим він більший, тим крутіша лінія регресії. У наведеному прикладі коефіцієнт m — це коефіцієнт чутливості ціни, який відбиває зміну частки ринку за зміни ціни.

На етапі перевірки якості моделі її оцінюють за адекватністю і точністю. Сенс такої перевірки полягає у тому, щоб обґрунтувати застосування методу функціонального аналізу для вивчення кореляційної залежності. Це буде правомірним лише у тих випадках, коли кореляційний (співвідносний) зв’язок не дуже віддалений від функціонального (жорсткого) зв’язку.

Оскільки модель відображує вплив на результативну ознаку лише частини реальних факторів, регресійний аналіз пояснює тільки частину дисперсії відгуку (загальної дисперсії). Таким чином:

.

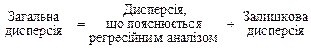Залишкова дисперсія — це та частина варіації залежної змінної, яку не можна пояснити впливом факторів, включених у регресійне рівняння.

Для оцінювання якості моделі і повноти набору пояснювальних факторів звичайно використовують коефіцієнт детермінованості R ². Його ще називають величиною вірогідності апроксимацїї, або рівнем надійності. Коефіцієнт детермінованості — це відношення дисперсії, що пояснюється регресійним аналізом, до загальної дисперсії. Він звичайно обчислюється за формулою

R² = SS_рег / (SS_рег + SS_зал),

де SS _рег = å(y (х_і) – у _сер)² — сума квадратів відхилень рівнів вихідного ряду даних від його середнього значення;

SS _зал — сума квадратів рівнів залишкової компоненти.

Коефіцієнт детермінації дає кількісну оцінку міри аналізованого зв’язку. Він показує частку варіації результативної ознаки, що знаходиться під впливом факторів, що вивчаються, тобто визначає, яка частка варіації ознаки у враховується у моделі й обумовлена впливом на неї незалежних факторів. Чим ближче R ² до 1, тим у більшому ступені рівняння регресії пояснює аналізований фактор (за функціонального зв’язку R ² дорівнює 1, а за відсутності зв’язку — 0). Якщо, наприклад, R ² дорівнює 0,9, то можна вважати, що 90 % змін (варіацій) у відгуку обумовлюються варіаціями в урахованих факторах і лише 10 % — за рахунок впливу інших факторів. Величина R називається індексом кореляції (множинне R). Цей коефіцієнт, як і R ², є універсальним, оскільки відбиває щільність зв’язку й точність моделі і може використовуватися за будь-якої форми зв’язку. За прямолінійного зв’язку індекс кореляції дорівнює коефіцієнту кореляції (r).

Для полегшення висновків щодо практичної значимості синтезованої моделі показникові щільності зв’язку дається якісна оцінка. Це здійснюється на основі шкали Чеддока:

Показник щільності зв’язку r	0,1—0,3	0,3—0,5	0,5—0,7	0,7—0,9	0,9—0,99
Характеристика сили зв’язку	Слабка	Помірна	Помітна	Значна	Вельми значна

Виходячи з величини індексу детермінації маємо, що у разі значної залежності результативної ознаки від факторів більше половини загальної варіації відгуку пояснюється впливом факторів, що вивчаються. Це дозволяє вважати виправданим застосування методу функціонального аналізу для вивчення кореляційного зв’язку, а синтезовані при цьому математичні моделі визнаються придатними для практичного використання. Якщо значення показника щільності зв’язку нижче 0,7, то величина індексу детермінації завжди буде менше 50 %. Це означає, що на частку варіації факторів, що вивчаються, припадає менша частина порівняно з іншими факторами, що впливають на змінну загальної дисперсії результатної ознаки. Синтезовані за таких умов математичні моделі практичного значення не мають. Але високий рівень показників щільності зв’язків не є гарантією того, що фактори, включені в модель, дійсно є основними. Може статися так, що вони лише відбивають вплив інших, глибинніших факторів. Так, чисельність населення може бути в дійсності важливішим фактором, ніж величина доходу споживачів.

Для перевірки міри точності застосовують незміщену оцінку дисперсії залишкової компоненти

МS _зал = SS _зал / df,

де df — ступінь вільності, що дорівнює N – m – 1 (N — кількість спостережень, m — кількість незалежних факторів).

Квадратний корінь з цієї величини називається стандартною помилкою оцінки. Для регресійного рівняння в цілому вона виступає як ступінь точності прогнозів, що базуються на рівнянні. Так, для розглядуваного прикладу з її допомогою можна визначити ймовір­ність того, що дійсний рівень частки ринку знаходитиметься в кон­кретному інтервалі близько до значення, яке виводиться з рівняння. Чим більше незалежна змінна відрізняється від середньої за спосте­реженнями, використовуваними для оцінки коефіцієнтів, тим більша невизначеність у прогнозі, що базується на рівнянні регресії.

Для перевірки значущості моделі регресії використовується F-критерій Фішера (F-відношення), обчислюваний за формулою

F₀ = МS_рег / МS_зал,

де МS _рег = SS _рег / m.

Якщо обчислене значення F -критерію більше за його критичне значення, що визначається за таблицею, то значення коефіцієнта детермінованості визнається суттєвим (невипадковим), а модель — значущою. За визначення критичного значення F -критерію враховується прийнятий рівень значущості (0,05 або 0,01) і число ступенів вільності df ₁ і df ₂ (df ₁ = m, df ₂ = N – m – 1).

Слід також проаналізувати значущість окремих коефіцієнтів регресії, тобто виявити, наскільки обчислені параметри регресійного рівняння характерні для конкретного комплексу умов, чи не є отримані значення параметрів рівняння регресії дією випадкових причин. Для вивчення кореляційного зв’язку показників ринкової діяльності це особливо важливо, оскільки розглядаються сукупності, які звичайно мають порівняно невелику кількість елементів. Це здійснюється з допомогою t -статистики шляхом перевірки гіпотези про рівність нулеві відповідного параметра рівняння. Якщо обчислене значення t -критерію з (N – m – 1) ступенями вільності перевищує його табличне значення за заданого рівня значущості, коефіцієнт регресії вважається значущим. У противному разі фактор, що відповідає такому коефіцієнту, слід вивести з моделі (при цьому її якість не погіршиться).

Важливу роль в оцінюванні впливу факторів відіграють коефіцієнти регресійного рівняння. Проте безпосереднє їх порівняння недопустиме з таких причин:

— значення коефіцієнта регресії залежить від одиниць його вимірювання. Якщо витрати на рекламу виражено у тисячах гривень, то можна довільно збільшити коефіцієнт шляхом заміни одиниці вимірювання на десятки тисяч, сотні тисяч і т. д.;

— незалежні фактори звичайно мають різну коливність (різні варіації);

— незалежні фактори зв’язані не тільки з результатним, а й деякою мірою і між собою. Отже, навіть якщо попередні причини не заважають прямому зіставленню коефіцієнтів, кожен з них не є «чистою» мірою впливу відповідного фактора на результатну ознаку.

У загальному випадку для того щоб зробити коефіцієнти регресії порівнянними, використовують часткові коефіцієнти елас­тичності, b-коефіцієнти регресії та коефіцієнти часткової (парної) кореляції.

Коефіцієнт еластичності показує, на скільки процентів зміниться результативна ознака за зміни j -го фактора на 1 %, якщо значення решти факторів фіксується на деякому рівні. Якщо за такий рівень узяти середні значення факторів, то отримаємо середній коефіцієнт еластичності

Е_j = m_j · X_{j cеp} / Y_cеp .

Вадою коефіцієнтів еластичності є те, що вони не враховують ступінь коливності факторів.

Бета-коефіцієнт (b-коефіцієнт) показує величину зміни результатної ознаки в значеннях середньої квадратичної помилки за зміни j -го фактора на одну середньоквадратичну (стандартну) помилку у разі фіксації значень решти факторів:

b_j = m_j · s_j / s_y .

Парний коефіцієнт кореляції r_j — це показник, що характеризує щільність зв’язку між результатною ознакою та j -м фактором за елімінації (виключення впливу) всіх інших факторів.

Зазначені коефіцієнти дають змогу зробити ранжування факторів за ступенем їх впливу на залежну змінну. Оцінити частку впливу j -го фактора у сумарному впливі всіх факторів, включених у регресію, можна за значенням дельта-коефіцієнта (D j) цього фактора:

Dj = r_j · b_j / (r₁ · b₁ + r₂ · b₂ + … + r_m · b_m).

Інший спосіб оцінювання важливості певного фактора полягає в оцінюванні зміни коефіцієнта детермінації при додаванні або виключенні з рівняння регресії цього фактора.

Excel забезпечує ефективну підтримку побудови та аналізу регресійних моделей: 15 функцій робочих аркушів, створених саме з цією метою, а також такі можливості, як побудова лінії тренда на графіках, та інструмент аналізу Регресія, з допомогою яких зручно проводити конкретні регресійні обчислення.

Найбільш наочний спосіб дослідження зв’язку між двома змінними базується на використанні точкової діаграми з лінією тренда. Крім того, Excel має набір спеціальних функцій, які за певних умов у використанні зручніші за діаграми.

Так, для обчислення значення R ² можна використати функцію КВПИРСОН.

Відрізок на осі ординат можна отримати з допомогою функції ОТРЕЗОК. Коефіцієнт нахилу лінійної регресії — за допомогою функції НАКЛОН. Щоб отримати відрізок на осі координат і коефіцієнт нахилу з допомогою однієї функції, слід виділити дві клітини, натиснути на панелі інструментів кнопку Вставка функції, у діалоговому вікні вибрати функцію ЛИНЕЙН, вказати перші два параметри (діапазон клітин, де знаходяться значення відгуку, та діапазон клітин зі значеннями незалежної змінної) і, тримаючи натиснутими клавіші Ctr і Shift, натиснути клавішу Enter.

Одночасно з обчисленням параметрів лінійного рівняння регресії (у тому числі й множинної) функція ЛИНЕЙН може повертати додаткову регресійну статистику. До цієї статистики входять:

se ₁, …, se_n — стандартні значення помилок для коефіцієнтів m ₁, …, m_n;

se_b — стандартне значення помилки для постійної b;

R ² — величина вірогідності апроксимацїї (коефіцієнт детермінації);

se_y — стандартна помилка для оцінки у;

F — F -статистика, або F -відношення;

df — кількість ступенів вільності (N – m – 1);

SS _рег — регресійна сума квадратів;

SS _зал — залишкова сума квадратів.

Розглянемо технологію проведення регресійно-кореляційного аналізу з допомогою Excel на конкретному прикладі. Припустимо, що треба дослідити результати збільшення витрат на рекламу деякої продукції і зниження ціни на одиницю цієї продукції з метою збільшення обсягів продажу. Почнемо з перевірки пропозиції про збільшення витрат на рекламу. Звичайно, не можна не враховувати того, що реальний продаж додаткових обсягів продукції може навіть не виправдати витрат на рекламну кампанію. Для з’ясу­вання цього питання слід виявити зв’язок між витратами на рекламу для кожного виду продукції і кількістю одиниць продаваної продукції. Якщо є необхідні дані для проведення регресійного аналізу, то цей зв’язок можна оцінити у кількісній формі.

На рис. 2.3.4 наведено таблицю, що має дві колонки — витрати на рекламу і кількість одиниць проданої продукції. Зв’язок між цими змінними можна легко (хоча і в дещо спрощеній формі) оцінити з допомогою точкової діаграми.

Для побудови цієї діаграми слід виділити дані в діапазоні А2:В20, вибрати команду Вставка / Діаграма (або клацнути на кнопці Майстер діаграм) і ввести потрібну інформацію на кожному з чотирьох кроків побудови діаграми. Зауважимо, що на першому кроці вибирається тип діаграми, яка має назву Точкова.

Коли діаграма з’явиться у робочому аркуші, треба клацнути по ній лівою кнопкою миші і вибрати команду Діаграма / Додати лінію тренда. У діалоговому вікні Лінія тренда на вкладці Тип вибирається тип апроксимації Лінійна, а на вкладці Параметри встановлюються режими: Показувати рівняння на діаграмі та Розмістити на діаграмі величину вірогідності апроксимації (R^2).

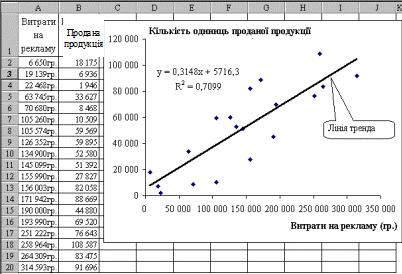
Рис. 2.3.4. Зв’язок між обсягами продажу (в одиницях продукції) і витратами на рекламу

На рис. 2.3.4 лінію тренда подано прямою, яка йде з нижнього лівого кута у правий верхній. Це говорить про те, що за збільшення витрат на рекламу пропорційно збільшуються й обсяги продажу (в одиницях продукції).

Діаграма також вміщує рівняння

у = 0,3148x + 5716,3.

Це рівняння регресії. Воно найкраще апроксимує дані, наведені у робочому аркуші, у вигляді прямої (y = mx + b). Для даного прикладу таке рівняння показує залежність між сумою грошей, витрачених на рекламу певної продукції, і обсягами продажу в одиницях цієї продукції (у — це обсяги продажу, x — витрати на рекламу в гривнях). Це не означає, що за відомих витрат на рекламу можна точно визначити обсяги продажу. Наприклад, у разі підстановки в рівняння замість х значення 171 942 грн (сума витрат на рекламу) буде отримано результат — 59843,64 одиниць продукції. У таблиці з даними значення 171 942 грн наведено як один з фактичних результатів спостереження, але цьому значенню відповідає зовсім інша величина обсягів продажу — 88 669 одиниць продукції. Отже, регресія на основі тих даних, які ми маємо, дає найбільш точну оцін­ку, але не абсолютно точний прогноз. Точність апроксимації з допомогою прямої залежить від ступеня розкиду даних. Чим ближче дані до прямої, тим точнішою є лінійна регресійна модель.

Розглядаючи принципи регресійного аналізу, дуже важливо зрозуміти, що регресія виражає зв’язок між змінними, а це не те саме, що причинна обумовленість, яка означає, що маніпуляції з однією змінною обов’язково приведуть до певних змін іншої.

Якщо в дане рівняння регресії підставити значення 400 000 грн, то отримаємо, що приблизний обсяг продажу в одиницях продукції дорівнюватиме 531636. Це зовсім не означає, що, витративши на рекламу 400000 грн, підприємство продасть 531 636 одиниць цієї продукції (хоча, звичайно, цього і не можна виключати). Є велика кількість факторів, крім витрат на рекламу, які впливають на зміни в обсягах продажу, і ці фактори (наприклад, продажна ціна одиниці продукції) у цьому рівнянні регресії ніяк не відображені. Навіть якщо зв’язок між змінними має причинний характер, треба ще знати напрям цієї причинності. Цілком вірогідно, що відділ маркетингу збіль­шував витрати на рекламу продукції після того, як збільшувались обсяги продажу. У цьому разі ми можемо бути впевненими лише у впливі обсягів продажу на розміри витрат на рекламу, а не навпаки.

Коефіцієнт регресії m є мірою нахилу лінії тренда: чим він біль­ший, тим крутіша лінія тренда. У даному разі — це число 0,3148. Воно інтерпретується так: «Якщо між обсягами продажу та витратами на рекламу є зв’язок, то, за попередніми оцінками, за збільшення витрат на рекламу на 10 000 грн буде продано додатково приблизно 3148 одиниць продукції».

Незмінна b — це відрізок на осі ординат. Вона вказує, в якому місці лінія тренда перетинає вісь у (вертикальну вісь). У даному разі — це число 5716,3. Воно інтерпретується так: «Якщо між обсягами продажу та витратами на рекламу є зв’язок і якщо не виділятимуться гроші на проведення реклами, то, за попередніми оцінками, буде продано приблизно 5716 одиниць продукції».

Значення коефіцієнта детермінації на діаграмі дорівнює 0,7099. Це означає, що приблизно 71 % міри мінливості обсягу продажу одиниць продукції зв’язано з мірою мінливості витрат на рекламу.

На рис. 2.3.5 у діапазоні A2:C20 знаходяться дані спостережень про обсяги продажу (у _ф), які включають, крім витрат на рек­ламу (х ₁), ціни (х ₂), за якими продавалися рекламовані товари.

	A	B	C
	Витрати на рекламу (x 1), грн	Ціна (x 2), грн	Продана продукція (y ф), од.
	6 650	147,2	7 175
	19 139	158,5	5 836
	22 468	161,5	9 946
	63 745	103,2	23 627
	70 680	191,9	8 468
	105 60	134,9	20 509
	105 574	107,8	49 569
	126 352	155,8	35 895
	134 900	117,8	52 580
	145 099	100,7	65 392
	155 990	172,9	27 827
	156 003	95,6	72 058
	171 942	98,8	80 669
	190 000	105,5	44 880
	193 990	99,9	69 520
	251 222	76,8	98 643
	258 964	95,2	75 587
	264 309	119,7	83 475
	314 593	125,5	91 696

Рис. 2.3.5. Дані про обсяги продажу, витрати на рекламу та ціни на товари

Моделі парної кореляції між обсягами продажу цих товарів і їх цінами наведено на рис. 2.3.3. При виборі лінійної моделі маємо регресійне рівняння у = –744,5 х + 141432 з коефіцієнтом детер­мінації 0,5763. Слід звернути увагу на те, що коефіцієнт регресії від’ємний, а лінія тренда йде з верхнього лівого у нижній правий кут діаграми. Тобто маємо звичайну залежність обсягів продажу від ціни продукції: чим вища ціна, тим менша кількість продукції продається.

Найпростіший спосіб визначити в Excel залежність результатної ознаки від декількох факторів — використати інструмент Регресія, який повертає всю потрібну інформацію, згруповану у декілька таблиць.

Для отримання цієї інформації слід активізувати робочий аркуш з даними і виконати такі дії:

1. Виконати команду Сервіс / Аналіз даних.

2. У діалоговому вікні Аналіз даних зі списку Інструменти аналізу вибрати інструмент Регресія і натиснути кнопку ОК.

3. Після появи діалогового вікна Регресія потрібно:

1) у текстовому полі Вхідний інтервал Y встановити діапазон С2:С20 (увести з клавіатури або виділити мишею ці клітини у робочому аркуші);

2) у текстовому полі Вхідний інтервал X встановити діапазон А2:А20;

3) у поле Рівень надійності ввести число 95 (якщо воно там не стоїть);

4) перемикач Параметр виведення встановити в положення Новий робочий аркуш;

5) клацнути по кнопці ОК.

Результати (рис. 2.3.6), отримані з допомогою інструмента Регресія, містять всю потрібну інформацію. Так, у клітині В5 знаходиться значення параметра R ², а в В4 — значення множинного R, яке являє собою квадратний корінь з дисперсії (R ²). Це значення (0,9085) є коефіцієнтом кореляції і виражає кореляцію між кіль­кістю проданої продукції і отриманою комбінацією незалежних змінних. Воно означає, що приблизно 91 % міри мінливості кількості продажу продукції зв’язано з мірою мінливості ціни, за якою продається ця продукція, і розмірами витрат на її рекламу.

Значення R ² двофакторної моделі суттєво більше, ніж відповід­них однофакторних. Це свідчить про те, що остання модель набагато краще за попередні пояснює зміни результативної ознаки (обсяги продажу). Проте ще треба з’ясувати, чи не є цей результат випадковим. Припустимо, що в дійсності ніякого взаємозв’язку змінної у та змінних х немає. Величину ймовірності помилковості твердження про те, що є значний взаємозв’язок між змінними, приймемо рівною 0,05. Для ступенів вільності маємо: df ₁ = 2 (кіль­кість факторів), df ₂ = 16 (значення клітини B13). У будь-якому статистичному довіднику можна знайти, що F -критичне (для вказаних величин) дорівнює 3,36. Спостережуване F -значення більше 79 (клітина Е12), що значно більше за F -критичне значення 3,36. Отже, припущення про відсутність взаємозв’язку залежної та незалежних змінних не підтверджується.

	A	B	C	D	E	F	G
	ВЫВОД ИТОГОВ
	Регрессионная статистика
	Множественный R	0,95317
	R-квадрат	0,90854
	Нормированный R-квадрат	0,8971
	Стандартная ошибка	9941,79
	Наблюдения
	Дисперсионный анализ
		df	SS	MS	F	Значи-мость F
	Регрессия		1,57E+10	7,85E+09	79,4666	4,898E-09
	Остаток		1,58E+09
	Итого		1,73E+10
		Коэффи­циенты	Стандартная ошибка	t -статистика	P -значение	Нижние 95 %	Верхние 95 %
	Y -пересечение	61304,1	14182,96	4,355678	0,000490366	31237,591	69924,2
	Переменная X 1	0,24181	0,031717	7,623928	1,0298E-06	0,1745723	0,33337
	Переменная X 2	–383,28	87,99497	–4,3224	0,00052558	–569,8207	–52,2293

Рис. 2.3.6. Інформація, видана інструментом Регресія

Нормований R ², що знаходиться у клітині В6, ураховує кількість результатів спостережень і незалежних змінних. Якщо кількість спостережень відносно кількості незалежних змінних не досить велика, R ² має тенденцію відхилятися в бік підвищення. Нормова­ний R ² забезпечує інформацією про те, яке значення могло б бути отримано в іншому наборі даних, значно більшому за аналізований. Якщо б розглядуваний приклад базувався на значно більшій кількості спостережень, то нормований R ² і фактичний R ²не дуже різнилися б.

Діапазон A17:C19 містить детальну інформацію щодо членів регресії — постійної b (Y-пересечение) та коефіцієнтів регресії — та їх стандартних похибок.

У колонці t-статистика знаходяться стандартизовані (нормованi) зміннi, які представляють частку кожного члена рівняння в його стандартній похибці.

У колонці P-значення розташовано результати обчислень, які дають змогу перевірити, чи є отримані значення коефіцієнтів регресії дійсно корисними у разі оцінювання з їх допомогою кількості продажу. Ці результати уможливлюють висновок, що у даному разі за умови, що відповідний коефіцієнт реально має нульове значення, ймовірність отримати значення

| m ₂| = 383,28 не більша 0,0006 (або 6 шансів з 10 000),

m ₁ = 0,2418 приблизно 0,000001 (або 1 шанс з 1 000 000),

b = 61 304,11 не більша 0,0005 (або 5 шансів з 10 000).

А це підтверджує статистичну значущість отриманих коефіцієнтів регресії.

Останні колонки третього розділу результатів вміщують нижню і верхню границі 95-процентного рівня надійності як для постійної, так і для кожного коефіцієнта регресії. Тут треба звернути увагу на те, що жоден з трьох довірчих інтервалів не охоплює нульове значення. Це саме той результат, який і треба було очікувати, оскільки всі Р -значення, що знаходяться вище 5-процент­ного рівня, є значущими. Якщо б Р -значення дорівнювало 0,05 або більше, довірчий інтервал цього показника включав би нуль.

Отже, можна з 95-процентною впевненістю стверджувати, що всі показники регресії не є нульовими. З цього випливає, що незалежні змінні додають до рівняння регресії значущу інформацію і на основі даних про витрати на рекламу продукції та ціни, за якими вона продається, можна досить точно прогнозувати обсяги продажу.

Дата добавления: 2014-01-11