Помилка вибірки

Після проведення певної кількості спостережень отримують розподілення результатів (вибіркових оцінок) того самого істинного рівня (наприклад, низки характеристик населення). Це вибір­кове розподілення підлягає законові нормального розподілення, якщо вибірка достатньо велика. Оскільки істинний рівень може не збігатися з рівнем вибіркових характеристик, необхідно брати до уваги похибку вибірки. У цьому разі можна знайти ступінь вірогідності вибіркових характеристик.

У математичній статистиці значення середньої похибки визначається за формулою

,

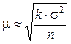де s² — дисперсія вибіркової сукупності;

n — чисельність одиниць вибіркової сукупності;

k — коефіцієнт, який для повторного відбору дорівнює одини­ці, а для безповторного — 1 – n / N, де N — чисельність генеральної сукупності.

Середня похибка вибірки використовується для визначення межі відхилень характеристик вибірки від характеристик генеральної сукупності. Суттєвим є твердження, що ці відхи­лення не будуть більші за значення, яке в статистиці нази­вається граничною помилкою вибірки, лише з певним ступенем імовірності.

Гранична помилка вибірки пов’язана із середньою похибкою вибірки співвідношенням

D = m × t,

де t — коефіцієнт кратності помилки.

Значення коефіцієнта кратності помилки залежить від того, з якою довірчою ймовірністю (надійністю) слід гарантувати результати вибіркового обстеження. Для його визначення користуються таблицею значень інтеграла ймовірностей нор­мального закону розподілення. В економічних дослідженнях звичайно обмежуються значеннями t, що не перевищують двох-трьох одиниць:

Кратність помилки	Імовірність (надійність)	Кратність помилки	Імовірність (надійність)	Кратність помилки	Імовірність (надійність)
0,1	0,0797	1,5	0,8664	2,6	0,9907
0,5	0,3829	2,0	0,9545	3,0	0,9973
1,0	0,6827	2,5	0,9876	4,0	0,999937

При цьому вибір тієї чи іншої довірчої імовірності залежить від того, з яким ступенем вірогідності слід гарантувати результати вибіркового обстеження (найчастіше спираються на ймовірність 0,9545, за якої t дорівнює 2).

Якщо в формулу для визначення D підставити конкретний вміст m, то для обчислення граничної помилки можна буде використати такі вирази:

- у разі альтернативної ознаки

,

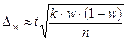де w — вибіркова частка, яка визначається з відношення одиниць, які мають досліджувану ознаку, до загальної чисельності одиниць вибіркової сукупності;

- у разі кількісної ознаки

,

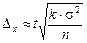де s² — дисперсія кількісної ознаки у вибірці.

Дата добавления: 2014-01-11