Из определения сразу следует, что

Следствие 5.

Для любых А, В Ì W,

Р { А È В } £ Р { А } + Р { В }.

Доказательство следует из условия Р { А Ç В } ³ 0 и следствия 4. _▼

Очевидны обобщения на произвольное число событий.

Определение. События А, В из вероятностного пространства (W,ℱ, Р) называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей этих событий, то есть

Р { А Ç В } = Р { А }× Р { В }.

1) Для любого А Ì W события А и W независимы.

2) Если Р { В } = 0 и событие А Ì W произвольно, то В и А независимы.

3) Если события А и В_i независимы, i = 1, 2 и В ₁ É В ₂, то А и (В ₁ В ₂) независимы.

4) Если события А и В_i независимы и В_i попарно несовместны, то есть " i ¹ j В_i Ç В_j = Æ, то А и также независимы.

5) Событие А не зависит от самого себя тогда и только тогда, когда либо , либо .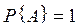

6) Если события А и В несовместны, то есть А Ç В = Æ и Р { А } > 0, , то А и В зависимы.

В самом деле, пусть события А и В независимы, тогда 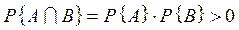, но по условию 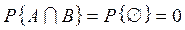. Получили противоречие, то есть А и В - зависимы._▼

Замечание 1. Понятие независимости в теории вероятностей имеет более глубокий смысл, чем независимость обычная. Принято считать события независимыми, если они не связаны причинно. На практике, понятие зависимости и независимости случайных событий относительно. Если события слабо связаны, и эта связь несущественно влияет на конечный результат, то такие события считают независимыми, поскольку в этом случае построение математических моделей реальных ситуаций становится много проще. Наиболее глубоко в теории вероятностей изучены именно независимые события.

Замечание 2. Из аксиоматического построения вероятности события следует, что событие случайно, если оно не достоверно и не невозможно. Это определение через отрицание и из него следует, что имеет смысл говорить о вероятности как о некотором определенном, но неизвестном нам числе. Утверждение, что вероятность события А существует, нуждается в обосновании, а если оно принято в качестве гипотезы, то в последующей проверке. Это следует учитывать при построении математических моделей реальных ситуаций.

Рассматривая вероятность события как число из промежутка [0,1], мы обычно предполагаем в какой его части это число будет находиться. И чем больше мы имеем информации о случайном событии, тем точнее предположение. Это позволяет нам определить вероятность как меру возможности (уверенности) появления случайного события.

Именно так Блез Паскаль в письме Пьеру Ферма в 1654 году написал: «Я считаю более простым и естественным принять степень уверенности в появлении достоверного события равной единице. Тем самым, возможность наступления случайных событий соизмеряется с тем, какую часть единицы они составляют».

Так впервые была формализована связь между случайным событием и числом, его измеряющим, – вероятностью.

Дата добавления: 2014-01-15