Часть 3. Предельные теоремы

Реальности нашей действительности подтверждают принцип, согласно которому определенного вида действия случайных событий, при весьма широких допущениях, приводят к результату, не являющемуся случайным. Благодаря этому принципу, законы теории вероятностей можно получать из закономерностей, присущих массовым случайным явлениям (событиям).

Некоторые законы можно сформулировать в виде предельных теорем, основывающихся на устойчивости среднего результата случайных факторов (например, оценка вероятности, числовых характеристик случайных величин, их распределений и др.).

Мы рассмотрим две группы предельных теорем.

К первой группе относятся теоремы, в которых, при определенным образом организованных условиях, доказывается сходимость случайных величин или функций от них к некоторым постоянным. Эта группа теорем носит название закона больших чисел. Примером может являться теорема Бернулли.

К другой группе предельных теорем относятся теоремы, использующие предельные свойства сумм случайных величин, где пределом последовательности частичных сумм являются не постоянные, а неслучайные функции (например, нормальное распределение или распределение Пуассона). В частности, в центральных предельных теоремах формулируются условия, при которых последовательности частичных сумм случайных величин сходятся к нормальному распределению

Замечание. Предельные теоремы и приближенные формулы (например, формула Пуассона) справедливы тогда, когда общее число испытаний заранее фиксировано. Если допустить, что, например, при подбрасывании монеты, игрок может закончить игру в выгодный для себя момент, то в целом результат игры не может быть оценен нормальным распределением, поскольку считается, что за достаточно длительное время произойдет любое, пусть и маловероятное, но мыслимое событие, то есть при n ® ¥ вероятность любому событию произойти близка к единице.

Докажем некоторые неравенства, которые, может быть, малопригодны на практике, в силу своей общности, но очень важны и эффективны в теоретических исследованиях.

Теорема. Для любой случайной величины x, с заданной функцией распределения F (x), имеет место неравенство

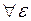>0, £ (110)

Доказательство. Пусть 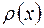- плотность случайной величины x, тогда имеем цепочку неравенств

._▼

Следствие 1. Пусть случайная величина x положительно определена, тогда

Следствие 2. (Неравенство Чебышева). Если дисперсия случайной величины x существует, то

или

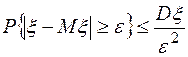. (111)

Дата добавления: 2014-01-15