Числовые ряды

Лекция №1

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии. - М.: Высшая школа, 1985. – 327 с.

2. Боровков А.А. Теория вероятностей, - М.: Наука, 1986. – 432с.

3. Вентцель Е.С. Теория вероятностей. - М.: Высшая школа, 2002. - 576 с.

4. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2002. – 479 с.

5. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1988. – 446с.

6. Карлин С. Основы теории случайных процессов. - М, «Мир», 1971.

7. Кафаров В.В., Дорохова И.Н., Арутюнов С.Ю. Системный анализ процессов химической технологии. – М.: Наука, 1985. – 440 с.

8. Клейнрок Л. Теория массового обслуживания. - М.: Машиностроение, 1979. – 432 с.

* Мы рассматриваем дискретное пространство, являющееся частным случаем более общего пространства элементарных событий. Для изучаемого курса теории вероятностей этого достаточно. Более общие случаи будем оговаривать особо.

* О независимости случайных величин смотри ниже

* Последовательность { x_n } сходится по вероятности к x, если для всякого e >0, Р {| x_n-x | >e}®0 при n ®¥. Формула (113) определяется как сходимость по вероятности дополнительной вероятности к событию {| x_n-x |£e}.

1. Понятие сходимости числового ряда

Пусть 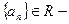последовательность действительных чисел,

- числовой ряд (1).

Составим последовательность частичных сумм:

последовательность частичных сумм

Если для ряда (1) существует предел последовательность частичных сумм при 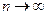, равный числу 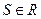, то ряд называется сходящимся, а число S – его сумма. В противном случае ряд (1) называется расходящимся.

Пример. Исследовать сходимость и найти сумму ряда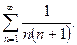

Составляем последовательность частичных сумм:

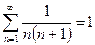
1. Свойства сходящихся рядов

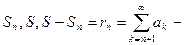остаток сходящегося ряда, последовательность остатка.

1. Необходимое условие сходимости: частичные суммы сходящегося ряда – ограничены: (это вытекает из того, что сходящаяся последовательность ограничена).

Приведём пример ряда, у которого частичные суммы ограничены, а сам ряд будет расходиться:

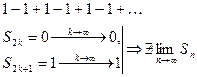
2. Необходимое условие сходимости: у сходящегося ряда предел общего члена равен нулю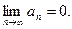

Доказательство. Доказано.

Рассмотрим пример расходящегося ряда, для которого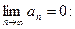

неограниченная, наименьшее слагаемое .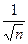

Пример. расходится, т.к.

Предположим, что

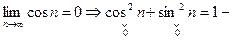противоречие.

3. Необходимое условие сходимости: у сходящегося ряда

Доказательство. 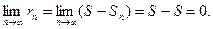Доказано.

4. Сходимость ряда не нарушится, если добавить или отбросить конечное число слагаемых.

5. Множество сходящихся радов образуют линейное пространство:

если

6. Критерий Коши: ряд (1) сходится фундаментальная, т.е.

Пример. 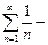гармонический ряд (расходящийся).

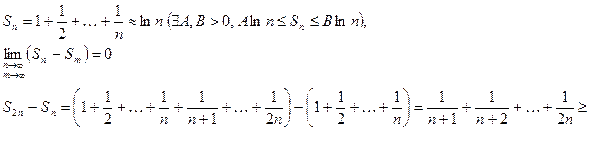
т.е. не выполнен критерий Коши, ряд расходится.

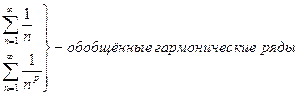
-функция Римана

Задача. Исследовать сходимость ряда 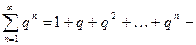сумма бесконечной геометрической прогрессии. Доказать, что при ряд сходится,

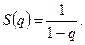
Решение.

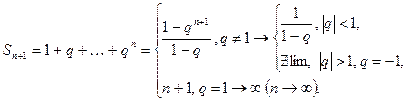
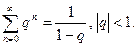
Дата добавления: 2014-01-15