
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм обучения по правилу Хебба
|
|
|
|
Персептронные алгоритмы обучения
Данный алгоритм положен в основу процесса обучения многих типов нейронных сетей.
Рассмотрим особенности применения правила Хебба к обучению НС.
Рассмотрим НС следующего вида:

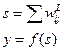
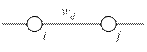
wij – весовой коэффициент связи нейронов i и j.
Предположим, что функция активации в выходном нейроне является пороговой. Для представления пороговой функции используется дополнительный вход с некоторым весовым коэффициентом b. Тогда выходной сигнал НС может быть вычислен следующим образом:
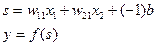 .
.
Процесс обучения НС состоит в настройке коэффициентов межнейронных связей и порогов при подаче на входы НС образов из обучающей выборки. Входной образ представляется в виде вектора X, каждая компонента которого подается на один из входов нейронной сети.
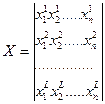
Значения коэффициентов межнейронных связей и порогов рассматриваемой НС на каждом шаге обучения (t, t +1,…) вычисляются с помощью следующих соотношений:
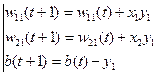 (*)
(*)
Различают алгоритм обучения в соответствии с правилом Хебба с учителем и без учителя. При обучении с учителем выходные сигналы НС сравниваются с эталонными значениями. При использовании алгоритма без учителя: реальные сигналы с выхода нейронной сети используются для кластеризации входных образов.
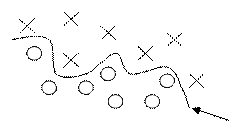 дискриминантная линия
дискриминантная линия
Таким образом, алгоритм обучения по правилу Хебба сводится к следующей последовательности действий:
1. Инициализация весовых коэффициентов и порогов случайными значениями, близкими к нулю (чтобы сеть сразу не могла войти в насыщение).
2. Подача на вход НС очередного входного образа.
3. Вычисление значения выхода.
4. Если значение выхода не совпадает с эталонным значением, то происходит модификация коэффициентов в соответствии с формулами (*). В противном случае осуществляется переход к пункту 5.
5. Если не все вектора из обучающей выборки были поданы на вход НС, то происходит переход к пункту 2. Иначе, переход к пункту 6.
6. Останов.
Правило Хебба не гарантирует сходимости процесса обучения, то есть ошибка аппроксимации функции нейронной сетью может превышать допустимое значение.
Основной недостаток алгоритма обучения по правилу Хебба заключается в том, что при увеличении размерности n входного вектора сходимость алгоритма уменьшается. При n > 5 трудно гарантировать сходимость.
Данный алгоритм, как правило, используется в качестве некоторого элемента в других алгоритмах обучения. Наиболее предпочтительным является использование правила Хебба в алгоритмах обучения без учителя.
Пример 1. Воспроизвести с помощью НС логическую функцию «ИЛИ». Будем проводить обучение в соответствии с правилом Хебба.
Примем значения сигналов биполярными: 1 и -1.
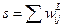
В соответствии с правилом Хебба инициализируем работу НС:
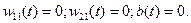
Вычисляем значение коэффициентов на каждом шаге:
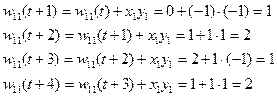
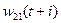 ,
, 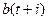 вычисляются аналогично.
вычисляются аналогично.
Результаты вычислений сведём в таблицу.
| шаг | x1 | x2 | x3 | y | w11 | w21 | b |
| t t+1 t+2 t+3 t+4 | – -1 -1 | – -1 -1 | – -1 -1 -1 -1 | – -1 | -1 -2 |
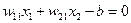
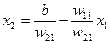 – дискриминантная линия
– дискриминантная линия
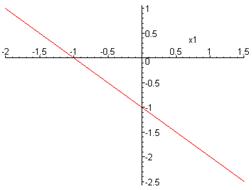
|
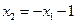
Алгоритм обучения Розенблатта
Данный алгоритм был положен в основу обучения однослойных персептронов.
Структура персептрона Розенблатта представляется следующим образом:
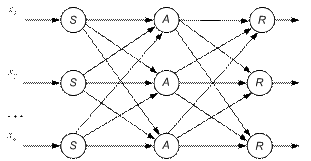
S -нейроны (сенсорные) – предназначены для формирования входных сигналов; выполняют чисто распределительную функцию. Каждый сенсорный нейрон связан с одним или несколькими нейронами следующего слоя (ассоциативными нейронами), при этом каждый ассоциативный нейрон может быть связан с несколькими S -нейронами.
A -нейроны (ассоциативные) – предназначены для непосредственной обработки входных сигналов. Выходы ассоциативных нейронов соединены с входами нейронов третьего слоя.
R -нейроны (эффекторные) – предназначены для передачи сигналов к другим нейронам или сетям. Нейроны этого слоя имеют несколько входов (дендритов) и один выход (аксон), который возбуждается, если суммарная величина входных сигналов превосходит порог срабатывания (функция активации нейронов – пороговая).
Отличия алгоритма обучения Розенблатта от алгоритма обучения по правилу Хебба сводятся к следующему:
1. вводится эмпирический коэффициент α с целью улучшения процесса сходимости: α – скорость обучения  ;
;
2. исключены некоторые действия, которые замедляют процесс обучения, например, обновление весовых коэффициентов (update).
3. входные образы на вход НС подаются до тех пор, пока не будет достигнута допустимая величина ошибки обучения.
4. если решение существует, алгоритм обучения Розенблатта сходится за конечное число шагов.
Алгоритм обучения персептрона Розенблатта заключается в настройке коэффициентов межнейронных связей и порогов в слое A. На каждом шаге обучения, если необходимо, происходит обновление весовых коэффициентов в соответствии со следующей формулой.
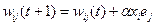 , (**)
, (**)
где t – номер такта; i – номер нейрона во входном слое; j – номер нейрона в слое A; α – скорость обучения; xi – входной сигнал; еj – ошибка обучения.
На каждом шаге обучения вычисляется ошибка обучения еj:
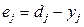 ,
,
где dj – эталонное значение входного сигнала; yj – реальное значение входного сигнала.
Алгоритм обучения Розенблатта сводится к следующей последовательности действий:
1. Инициализация весовых коэффициентов и порогов значениями, близкими к нулю.
2. Подача на вход НС очередного входного образа (входного вектора Х), взятого из обучающей выборки, и вычисление суммарного сигнала по всем входам для каждого нейрона j: 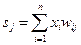 , где n – размерность входного вектора, xi – i -я компонента входного вектора, wij – весовой коэффициент связи нейрона j и входа i.
, где n – размерность входного вектора, xi – i -я компонента входного вектора, wij – весовой коэффициент связи нейрона j и входа i.
3. Вычисление значения выхода каждого нейрона:
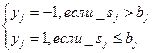 , где bj – порог, соответствующий нейрону j
, где bj – порог, соответствующий нейрону j
4. Вычисление значения ошибки обучения для каждого нейрона 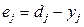 .
.
5. Проводится модификация весового коэффициента связи по формуле (**).
6. Повторение пунктов 2 – 5 до тех пор, пока ошибка сети не станет меньше заданной 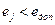 .
.
Особенности алгоритма обучения Розенблатта: должна быть задана скорость обучения α и ошибка обучения е.
Пример. Воспроизведение логической функции «И» с помощью НС. Обучение НС
производится в соответствии с алгоритмом обучения Розенблатта.
Значения сигналов – биполярные: 1 и -1. Задаём скорость обучения α = 1.
Инициализируем работу НС: 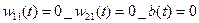
Вычисляем значение коэффициентов на каждом шаге:
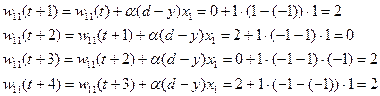
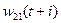 ,
, 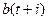 вычисляются аналогично.
вычисляются аналогично.
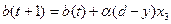
Результаты вычислений сведём в таблицу.
| шаг | x1 | x2 | x3 | y | d | w11 | w21 | b |
| t t+1 t+2 t+3 t+4 | – -1 - | – -1 - | – -1 -1 -1 -1 | – -1 -1 | – -1 -1 -1 | -2 |
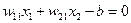
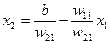 – дискриминантная линия
– дискриминантная линия
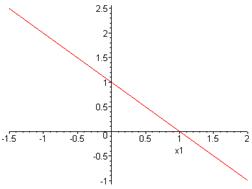
|
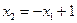
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 6808; Нарушение авторских прав?; Мы поможем в написании вашей работы!