Методы формирования популяции

Совокупность особей 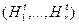образует популяцию 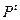(численностью r). Эволюция популяции 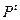рассматривается как чередование поколений. Номер поколения отождествляется с моментом времени t = 0,1,..., Т, где Т — жизненный цикл популяции, определяющий период ее эволюции. Совокупность генотипов всех особей 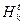образует хромосомный набор, который полностью содержит в себе генетическую информацию.

Наиболее известны три метода формирования популяции:

1) метод "одеяло" – известны все решения, среди них с помощью генетического алгоритма находят наилучшее;

2) метод "дробовик" – случайным образом формируется множество решений;

3) дублируется (улучшается) уже известное решение.

Способы представления хромосом:

1) представление возможных решений в виде двоичных строк (предложен Холландом, классический способ). При использовании двоичных строк наблюдается преждевременная сходимость (стагнация) – попадание в ловушку (локальный минимум). Необходимо генетическое разнообразие, а с другой стороны при работе алгоритма требуется сохранять наилучшего решения с точки зрения функции оценки.

2) представление хромосом в виде вещественных чисел.

3) представление хромосом с помощью кода Грея.

Селекция sl хромосом связана с выбором пары хромосом из популяции с целью аккумуляции всех лучших функциональных признаков, имеющихся в популяции.

Существует несколько способов селекции:

1. лучший с лучшим (сохранение лучшего решения);
2. лучший с худшим (получение генетического разнообразия);
3. случайный выбор.

Скрещивание осуществляется с помощью двух генетических операторов:

1) Оператор кроссинговера.

2) Оператор мутации.

Применяется для предотвращения потери важного генетического материала в процессе биологической эволюции.

Мутация m – изменение части хромосомы с целью получения другого решения.

Для двоичного представления меняется один из разрядов (0 на 1 или 1 на 0). Мутация, при которой меняется только один ген, называется генной. Существует хромосомная мутация.

В результате применения генетических операторов получаем новую популяцию (родители, потомки и мутанты).

Для сохранения популяции используется естественный отбор. Необходимо оценить все хромосомы популяции. Для этого используется функция оценки или функция фитнесса.

Функция фитнесса должна быть выражена в терминах фенотипа (а не генотипа).

.

Каждая переменная () должна быть представлена в явном виде.

Функция фитнесса – оценочная функция (оценивает значимость хромосомы для популяции).

Виды функции оценки:

1) аналитический вид;

2) специальные программы;

3) НС.

Обычно при работе генетического алгоритма размер получившейся популяции усекается до первоначального размера.

Заканчивается работа алгоритма:

1) при нахождении хромосомы заданного вида;

2) при завершении определённого числа итераций.

Дата добавления: 2014-01-15