Персептрона

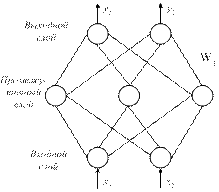
Применение генетического алгоритма к обучению многослойного

Основная (первая) задача: нахождение таких значений весовых коэффициентов, при которых минимизируется ошибка обучения (поиск глобального экстремума).

В качестве популяций используются НС с различными весовыми коэффициентами.

,

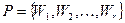где r – число НС, которые используются при выборе весовых коэффициентов, минимизирующих ошибку обучения .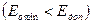

Алгоритм обучения:

1. Инициализация векторов 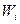, значениями, близкими к нулю.
2. Селекция: выбираются методы, хорошо себя зарекомендовавшие при оптимизации многопараметрических задач.
3. Применение генетических операторов кроссинговера и мутации.

Существует два подхода:

1) использование операторов на уровне генотипа (хромосомы);

2) использование операторов на уровне фенотипа.

1. Определение функции ошибки сети :

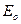по очереди на вход НС подаются входные образы и вычисляется 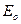конкретной сетью из популяции; на следующем этапе используются сети с наименьшими 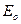; т. о. в качестве функции фитнесса используется .

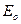Если для некоторой сети получили 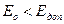, то выбирается данная НС в качестве решения.

На четвёртом этапе при использовании операторов на уровне фенотипов для вычисления 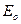предпочтительней использовать оператор мутации.

Процедура заканчивается если:

· ;

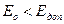· завершено определённое число шагов итерации. Если ошибка не получена, то переходим к НС с другой архитектурой, либо расширяем пространство поиска.

1. Тестирование НС на примерах, отличных от тех, которые используются на шаге 4.

Вычисляем ошибку обобщения .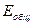

Основное отличие данного ГА от BP:

В силу свойства ГА, связанного с возможностью анализа параллельных решений, одновременно осуществляется поиск минимума многих сетей с одной (фиксированной) архитектурой. Таким образом, уменьшается время поиска решения, увеличивается вероятность нахождения глобального экстремума.

Вторая задача: нахождение минимального числа слоёв НС и числа нейронов в каждом слое.

Первая и вторая задачи оптимизации – поиск минимального 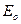и минимальной архитектуры – взаимно противоречивые, их необходимо решать совместно.

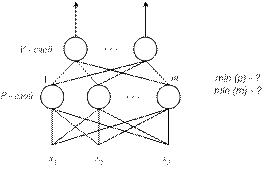
Для решения конкретной прикладной задачи строится своя НС. Сам тип НС, а также её архитектуру выбирает пользователь.

Желательно строить САПР НС, которая будет подбирать тип и архитектуру НС применительно к конкретной задаче.

Постановка задачи: задано количество входов НС 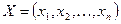; известно число выходов НС (количество классов). Необходимо определить число промежуточных слоёв НС и число нейронов в каждом слое.

Для построения НС, адекватной данной задаче, вводится интегральный критерий:

,

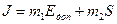где 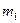, 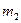- коэффициенты, определяющие вклад каждой составляющей, ;

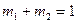S – суммарное количество связей.

Задача выбора архитектуры НС также может быть решена с помощью ГА. В этом случае решается задача перебора, а не задача непрерывной оптимизации. В качестве хромосомы может использоваться путь в графе.

Дата добавления: 2014-01-15