Оптимизации

Применение сети Хопфилда к решению задач комбинаторной

Рассмотрим задачу коммивояжера (классический пример NP -полной задачи):

На плоскости расположено N городов (в данном случае N =5). Необходимо, начиная с произвольного города, посетить все города, при этом в каждом побывать ровно один раз. Проблема заключается в выборе маршрута с минимально возможной длиной пути.

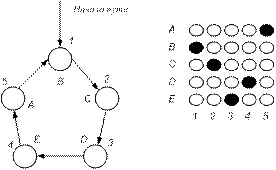
Для решения этой задачи может быть использована сеть Хопфилда, состоящая из 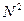нейронов, расположенных в виде матрицы 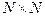нейронов: i -я строка матрицы соответствует i -му городу (одному из A, B, C, D, E), i -й столбец соответствует i -му порядку посещения города. Выход узла сети на пересечении строки x (A, B, C, D, E) и столбца i обозначим 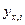, где x представляет город, а i – порядок посещения. Тогда один из возможных путей имеет вид:

.

Зачерченные 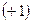и светлые 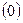кружки обозначают выходы узлов соответственно. Если , то это означает посещение города x на шаге i. Поскольку каждый город может быть посещён только один раз, то в матрице нейронов в каждом столбце и в каждой строке должно быть только по одному зачерченному кружку, соответствующему единичному выходу.

Расстоянием между городами x и y является: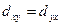, где .

Целевая функция E задачи поиска оптимального маршрута (функция энергии) может быть определена следующим образом:

(1)

, где 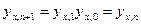; - положительные константы.

Первые три слагаемых вводятся для определения правил синтаксиса задачи. Необходимо минимизировать функцию цели, т.е. E должна быть равна 0, следовательно, все слагаемые должны быть равны 0.

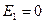, если имеется только один активный нейрон в каждом ряду, т.е. если каждый город посещается только один раз в каждом туре, иначе 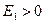. 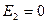, если имеется только один активный нейрон в каждом столбце, т.е. в каждый момент времени посещается только один город. 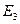определяет посещение N заданных городов в каждом туре. Таким образом, первые три слагаемых уравнения отвечают за допустимость маршрута: каждое из этих слагаемых обращается в нуль на допустимых маршрутах и принимает значение больше нуля на не допустимых.

Четвёртое слагаемое минимизирует длину маршрута. Отрезок пути между двумя городами включается в сумму только тогда, когда один из городов является относительно текущего города x либо предыдущим, либо последующим.

Приведём целевую функцию к основной форме уравнения сети Хопфилда – функции Ляпунова для двумерной 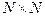нейронной матрицы:

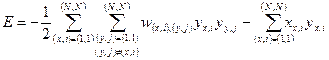. (2)

Путём сопоставления коэффициентов уравнения (1) и (2) можно определить весовые коэффициенты:

,

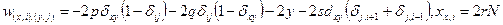где 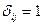при 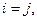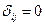- в противном случае.

Теперь алгоритм обучения Хебба можно заменить прямым заданием указанных весов для НС.

Дата добавления: 2014-01-15