Самоорганизация в НС

Самоорганизующиеся нейронные сети

Основная цель самоорганизации в НС – создание условий выживания организмов в определённых условиях.

Под самоорганизацией понимается процесс разбиения входного пространства на области (кластеры) таким образом, чтобы при поступлении новых данных в виде входных векторов их можно было идентифицировать (разнести по кластерам).

Для двухмерного пространства существует оптимальное разделение (Voronoj): правильные многоугольники, в узлах (в центре многоугольников) которых – нейроны. При подаче нового вектора на вход системы определяется расстояние между входным вектором и каждым из нейронов. При отнесении вектора к какому-либо классу точность определяется допуском.

С. Гроссбергом было доказано, что оптимальное разбиение существует только для двухмерного пространства. Также им были предложены определённые алгоритмы, с помощью которых можно разделить n -мерное пространство.

Для построения кластеров необходимо произвести обучение сети.

Различают обучение с учителем и без учителя. Ранее нами были изучены алгоритмы обучения с учителем. Рассмотрим алгоритмы обучения без учителя, которые также называются алгоритмами объективной классификации.

Для реализации алгоритмов обучения без учителя необходимо:

1. выбрать способ разбиения объектов на классы;

2. выработать правила отнесения входного образа к определённому классу.

НС, работа которых основана на использовании алгоритма объективной классификации, свойственен принцип самообучения или самоорганизации.

Суть самообучения:

1. при обучении правильные ответы сети не сообщаются;

2. во время процедуры обучения происходит формирование кластеров на основе обобщения имеющейся входной информации, сосредоточенной в обучающей выборке;

3. обученная сеть относит новый входной вектор к одному из кластеров, руководствуясь некоторым критерием сходства.

К НС, обучающимся без учителя (НС объективной классификации или НС с самоорганизацией), можно отнести следующие нейронные сети:

· сети Кохонена

· ART-сети

· ART MAP

Процесс разбиения некоторого множества объектов на классы с целью решения задач классификации и распознавания называется кластеризацией.

Процесс кластеризации реализуется в алгоритмах обучения без учителя.

Критерием разбиения служит некоторая мера близости или сходства. Кластеризация и обучение проводится на основе определённых математических методов, использующих соответствующие им математические модели пространства объектов.

Например, объекты – n -мерные векторы X = (x₁, x₂,…,x_n)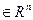, в качестве меры близости двух объектов Х₁ и Х₂ можно принять:

· евклидово расстояние между ними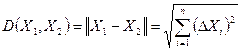

· максимальную разность значений компонент векторных описаний

· скалярное произведение двух векторов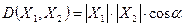

Введенные меры сходства могут служить критерием для отнесения некоторого объекта к соответствующему классу.

Дата добавления: 2014-01-15