Алгоритм максимального расстояния

Характерная особенность алгоритма – выбор наиболее удалённых кластеров.

Дано:

1. множество точек во входном пространстве X

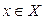
Данный алгоритм сводится к следующей последовательности действий:

1) Выбираем случайным образом точку, соответствующую центру первого кластера. (z₁)

2) Из множества точек X выбираем такую точку, которая наиболее удалена от точки, соответствующей центру z₁, и определяем эту точку как центр второго кластера.

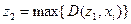
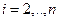
3) Для каждой из точек вычисляются расстояния от данной точки до всех центров кластеров , созданных на данный момент времени.

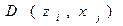
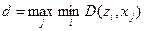
То есть для каждой точки x_j множества X определяется кластер («свой» кластер), расстояние до которого будет минимальным. Далее выбирается точка x^*, наиболее удалённая от данного («своего») кластера.

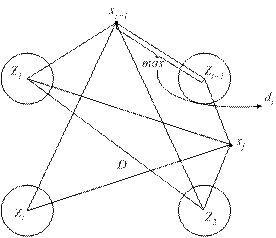
На каждом шаге алгоритма t= 1,2,3,…вычисляется величина: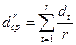

Если значение d составляет существенную часть (не менее половины) от величины 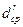, то тогда x^* объявляется центром нового кластера. В противном случае (значение d менее половины от величины 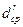) процесс завершается, а все оставшиеся точки множества X разносятся по ближайшим кластерам.

Недостатки алгоритма:

2. случайный выбор начального кластера

3. увеличение уровня сложности на каждом шаге работы алгоритма

3. Алгоритм внутригруппового среднего (метод K-средних, K-means clustering, C-means clustering)

Данный алгоритм минимизирует сумму квадратов расстояний между точками кластеров в процессе разбиения исходного пространства на q кластеров.

Дано:

1. множество точек во входном пространстве X

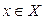
Алгоритм сводится к следующей последовательности действий:

1) Произвольно выбираются q центров кластеров (в качестве центров кластеров берутся точки из входного множества).

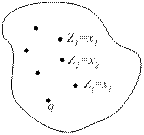
2) Все образы (точки из входного множества), не являющиеся центрами кластеров, «разносятся» по кластерам в соответствии с принципом минимального расстояния до центра кластера.

Образ х принадлежит кластеру K_j, если расстояние от точки х до центра z_j(r) данного кластера меньше расстояния от х до центра любого другого кластера (q- 1). K_j определяет множество, состоящее из точек, включённых в него до r -ого шага.

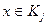, если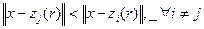

3) Определяются новые центры кластеров z_j(r+ 1 ), j= 1 … q таким образом, чтобы минимизировать показатель качества J.

В данном случае используется евклидово расстояние.

Новый центр кластера вычисляется по следующей формуле:

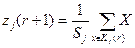, где – количество точек, включенных в пространство K_j к r-ому шагу итерации.

4) Алгоритм заканчивает свою работу, если выполняется равенство: , то есть не изменяются центры кластеров. В противном случае, переход к пункту 2.

Пример реализации алгоритма К-средних

Дано:

Х ={x₁, x₂,…,x₁₀}

q =3

Положим, что Z₁ = X₁; Z₂ = X₃; Z₃ = X₄

В технике оптимизации используется приём "мультстарт": алгоритм оптимизации реализуется несколько раз из различных начальных точек, а затем из полученных решений выбирается наилучшее.

Шаг 1. Определяем минимальное расстояние от каждой точки до каждого кластера.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
коорд.	(2;2)	(2;4)	(3;4)	(3;8)	(4;7)	(5;9)	(6;1)	(6;8)	(7;1)	(8;1)
Z1			-	-	5,4	7,6	4,1	7,2	5,1	6,05
Z2	-			-	3,2	5,4	4,2			5,8
Z3	-	4,1	-		1,4	2,3	7,6		8,05	8,6

Шаг 2. По критерию минимального расстояния определяем, какие точки относятся к какому кластеру.

кластер	точки
	X1, X7
	X2, X3, X9, X10
	X4, X5, X6, X8

Шаг 3. Пересчёт всех кластерных центров Z _i

Z₁ = (4; 1,5)

Z₂ = (5; 2,5)

Z₃ = (4,5; 8)

Шаг 4.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
Z1^1		3,2	2,7	6,6	5,5	7,6		6,8
Z2^1		3,35	2,5	5,85	4,6	6,5	1,8	5,6	2,5	3,4
Z3^1	3,5	4,7	4,3	1,5	1,1	1,1	7,2	1,5	7,4	7,8

Шаг 5.

кластер	точки
	X1, X2
	X3, X7, X9, X10
	X4, X5, X6, X8

Шаг 6.

Z₁² = (2; 3)

Z₂² = (6; 1,75)

Z₃² = (4.5; 8)

Шаг 7.

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
Z1^2			1,4	5,1	4,47	6,7	4,47	6,4	5,4	6,3
Z2^2		4,6	3,75	6,9	5,6	7,1	0,75	6,25	1,25	2,1
Z3^2	6,5	4,7	4,3	1,5	1,1	1,1	7,2	1,5	7,4	7,8

Шаг 8.

кластер	точки
	X1, X2, X3
	X7, X9, X10
	X4, X5, X6, X8

Если проводить дальнейшее разбиение, центры кластеров изменяться не будут.

4. Алгоритм нечётких K-средних (fuzzy C-means clustering)

Алгоритм предложен американским учёным Bezdek.

Fuzzy ISODATA

Твёрдые алгоритмы С-means (CM)

Hard C- means (HCM)

Основу алгоритма HCM составляет введение некоторой функции качества при заданных ограничениях.

Пусть U – матрица, определяющая принадлежность множества векторов X некоторым кластерам.

Дата добавления: 2014-01-15