Граничные условия в электростатическом поле

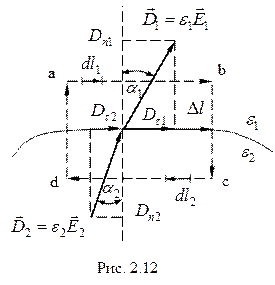При переходе через границу раздела сред векторы и 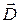изменяются скачком, т.к. скачкообразно изменяется диэлектрическая проницаемость .

При решении задач часто необходимо знать, как ведут себя векторы и 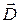на границах раздела сред, т.е. знать граничные условия.

Под граничными условиями в электрическом поле понимают условия на тех поверхностях, где и 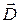претерпевают скачкообразные изменения, или на которых значения этих величин известны.

Пусть поверхность является границей раздела двух однородных и изотропных сред с диэлектрическими проницаемостями и 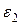(рис. 2.12). Выберем на поверхности раздела двух сред элемент дуги и построим контур abcd на этом элементе дуги. Выберем произвольно направление обхода контура. Циркуляция вектора по замкнутому контуру равна нулю (поле потенциальное) (2.23)

.

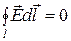Устремляя ad и bc к нулю, получим

,

откуда

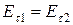, (2.37)

где 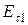и - касательные (тангенциальные) составляющие вектора на поверхности раздела (при наличии поверхностного заряда соотношение такое же).

Таким образом, тангенциальные составляющие вектора при переходе через поверхность раздела двух сред вне зависимости от наличия заряда на поверхности раздела не терпят разрыва.

Так как , то

, (2.38)

т.е. тангенциальная составляющая вектора электрической индукции на границе раздела двух сред терпит разрыв, изменяется прямо пропорционально диэлектрической проницаемости сред вне зависимости от наличия заряда на поверхности раздела.

Поведение нормальных составляющих и можно определить при помощи теоремы Гаусса в дифференциальной форме, записанной для поверхности раздела (2.34) при замене объемного заряда с удельной плотностью 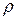на поверхностный заряд с плотностью .

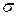Уравнение 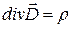для поверхности раздела примет вид

,

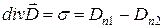где - поверхностная дивергенция, которая определяет поведение нормальных составляющих вектора 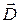на поверхности раздела сред.

Так как , получим

.

В частном случае, если 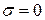, то для нормальных составляющих векторов 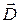и имеем

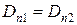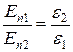; . (2.39)

Выводы:

а) при наличии поверхностного заряда:

, ;

, ;

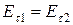б) при отсутствии поверхностного заряда:

, ;

, .

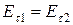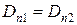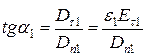, , а отношение

.

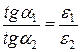Эта формула выражает закон преломления линий векторов 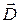и при переходе из одной среды в другую при отсутствии поверхностного заряда.

Дата добавления: 2014-01-15