
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энергия электрического поля
|
|
|
|
Поле любой системы зарядов обладает энергией. Определим энергию системы двух точечных зарядов. В точке 1 находится заряд 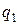 . Потенциал поля заряда q 1 в точке 2 равен
. Потенциал поля заряда q 1 в точке 2 равен 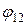 . Поместим заряд
. Поместим заряд 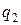 в точку 2. Энергия заряда
в точку 2. Энергия заряда 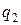 в точке 2 -
в точке 2 - 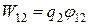 . Это работа, которую может выполнить поле при перемещении заряда
. Это работа, которую может выполнить поле при перемещении заряда 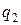 из точки 2 в бесконечность. Потенциал точки 1 в поле заряда
из точки 2 в бесконечность. Потенциал точки 1 в поле заряда 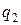 равен
равен 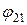 и энергия заряда
и энергия заряда 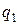 в точке 1 -
в точке 1 - 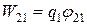 .
.
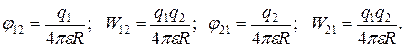
Следовательно, энергия взаимодействия зарядов 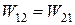 .
.
Для удобства энергию записывают в симметричной форме
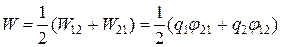 . (2.41)
. (2.41)
Если имеется система зарядов, то
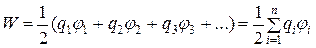 , (2.42)
, (2.42)
где 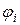 - потенциал в точке расположения заряда q i, созданный всеми оставшимися зарядами, кроме q i. Последнее равенство не определяет полную энергию системы, т.к. в нем не учитывается энергия, затраченная на создание зарядов.
- потенциал в точке расположения заряда q i, созданный всеми оставшимися зарядами, кроме q i. Последнее равенство не определяет полную энергию системы, т.к. в нем не учитывается энергия, затраченная на создание зарядов.
Если поле возбуждается объемным зарядом, то за точечный заряд можно принять 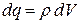 , если поверхностным, то
, если поверхностным, то 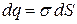 и энергия
и энергия
 или
или 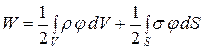 .
.
Если потенциал 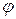 в первом слагаемом создан только объемным зарядом, а во втором – только поверхностным, то равенство определяет сумму собственных энергий.
в первом слагаемом создан только объемным зарядом, а во втором – только поверхностным, то равенство определяет сумму собственных энергий.
Если потенциал 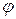 в первом слагаемом создан только поверхностным зарядом, а во втором – только объемным, то равенство определяет взаимную энергию.
в первом слагаемом создан только поверхностным зарядом, а во втором – только объемным, то равенство определяет взаимную энергию.
Если потенциал 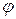 в первом и втором слагаемых создан объемным и поверхностным зарядами, то равенство определяет полную энергию системы.
в первом и втором слагаемых создан объемным и поверхностным зарядами, то равенство определяет полную энергию системы.
Все приведенные выражения для энергии электрического поля справедливы для стационарного поля. Они указывают на то, что энергия сосредоточена в местах распределения зарядов, что противоречит материалистическому пониманию поля. Поэтому эти формулы, являясь удобным математическим аппаратом, не отражают сущности явления.
Энергией обладает электромагнитное поле, покажем это.
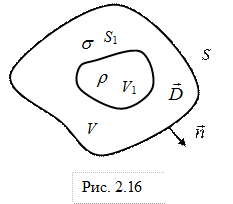 Рассмотрим объем V, в котором имеется и объемный и поверхностный заряды (рис. 2.16).
Рассмотрим объем V, в котором имеется и объемный и поверхностный заряды (рис. 2.16).
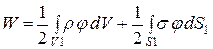 .
.
Учитывая, что 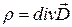 и
и 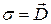 (т.к. напряженность электрического поля на внешней поверхности проводника (2.40) определяется как
(т.к. напряженность электрического поля на внешней поверхности проводника (2.40) определяется как 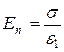 ), получим
), получим
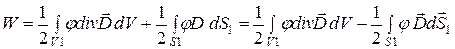 ,
,
т.к. 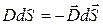 .
.
Применив теорему Остроградского, получим

Здесь 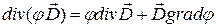 и
и 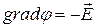 .
.
Таким образом,
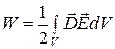 . (2.43)
. (2.43)
Формула справедлива и для стационарных и для переменных полей.
Уравнение показывает, что носителем энергии является электростатическое поле. Энергия электростатического поля распространяется во всем пространстве.
В однородных и изотропных средах  , тогда
, тогда
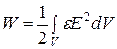 , (2.44)
, (2.44)
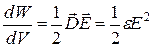 .
.
Энергия единицы объема 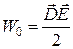 . (2.45)
. (2.45)
Измеряется энергия в джоулях (Дж).
Если имеется заряженный проводник с зарядом q, то 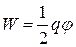 , но т.к.
, но т.к. 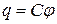 , то
, то 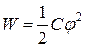 или
или
 . (2.46)
. (2.46)
Зная энергию, можно определить силу, действующую на заряженный проводник 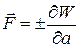 , где F - обобщенная сила, а – обобщенная координата – координата, вдоль которой происходит результирующее бесконечно малое перемещение под действием силы F.
, где F - обобщенная сила, а – обобщенная координата – координата, вдоль которой происходит результирующее бесконечно малое перемещение под действием силы F.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 348; Нарушение авторских прав?; Мы поможем в написании вашей работы!