Плоская электромагнитная волна

Плоские электромагнитные волны

Под плоской электромагнитной волной понимают волну, векторы и 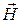которой расположены в плоскости хоу,перпендикулярной направлению распространения волны (оси z), и изменяются только в функции координаты z и времени t. На рис. 6.1 для одного и того же момента времени изображены векторы и 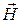в двух параллельных плоскостях, перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости (рис. 6.1, а) напряженность электрического (магнитного) поля одинакова по величине и по направлению. Во всех точках второй плоскости (рис. 6.1, б) напряженность электрического (магнитного) поля также одинакова по величине и по направлению, но она не равна напряженности поля в первой плоскости. В силу самого определения плоской волны

. (6.1)

В плоской волне и 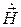являются функциями только одной координаты, в нашем случае функцией только координаты z.

Повернем координатные оси таким образом, чтобы ось у совпала с напряженностью магнитного поля 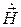. При этом

,

где 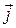- единичный орт оси у декартовой системы координат.

Подставим 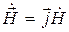в уравнение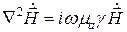(5.30) и раскроем оператор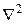

.

Учтем, что

и .

Поэтому

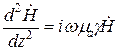. (6.2)

В уравнении вместо частной производной стоит простая производная, т.к. 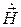является функцией только переменной z.

Это линейное дифференциальное уравнение второго порядка. Его решение

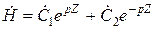, (6.3)

где 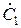и - постоянные интегрирования, комплексные величины, которые находятся из граничных условий и определяются для конкретной задачи;

Из характеристического уравнения 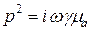найдем постоянную распространения

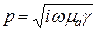. (6.4)

Если единица измерения - (Ом×м)^-1, 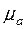- Гн/м, то измеряется в м ^-1.

Как было показано ранее

, где . (6.5)

Найдем напряженность электрического поля . Для проводящей среды первое уравнение Максвелла в комплексной форме имеет вид

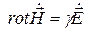. Отсюда .

С учетом того, чтои 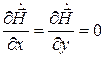, получим

, следовательно,

. (6.6)

Производная

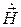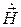Выражение (6.6) показывает, что напряженность электрического поля в плоской волне при выбранном расположении осей координат направлена вдоль оси х, о чем свидетельствует присутствие единичного орта оси х (орта ). Таким образом, в плоской электромагнитной волне между векторами и есть пространственный сдвиг в 90⁰ (направлено по оси х, а - по оси у).

Частное от деления на 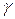называется волновым сопротивлением

. (6.7)

Волновое сопротивление определяется в омах (Ом), зависит от свойств среды и угловой частоты.

Проекция на ось х равна

,

где и .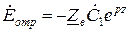

Проекция 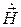на ось у равна

,

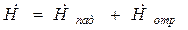где и .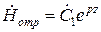

Составляющие падающей волны и определяют вектор Пойтинга (см. рис. 6.2, а). Он направлен вдоль положительного направления оси z. Следовательно, движение энергии с падающей волной происходит вдоль положительного направления оси z.

Составляющие отраженной волны 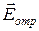и определяют вектор Пойтинга (см. рис. 6.2, б). Он направлен вдоль отрицательного направления оси z. Следовательно, движение энергии с отраженной волной происходит вдоль отрицательного направления оси z.

Волновое сопротивление можно трактовать как отношение .

Волновое сопротивление является числом комплексным и имеет аргумент 45⁰, поэтому сдвиг во времени между и для одной и той же точки поля равен четверти периода.

6.2.Распространение плоской электромагнитной волны

Дата добавления: 2014-01-15