Лекция № 8. Обработка результатов методом математической статистики

Обработка результатов методом математической статистики.

Обычно аналитик имеет реальное число (n<20) результатов, которое называют выборочной совокупностью. Перед обработкой данных необходимо выявить промахи и исключить их из числа рассматриваемых результатов выборочной совокупности. Для этого используется достаточно простой метод с применением Q-критерия. Суть метода заключается в расчете величины Q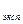, равной отношению выпадающего и ближайшего к нему результата к размаху варьирования (разности наибольшего и наименьшего из результатов выборочной совокупности) и в сравнении Q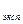с критическим значением Q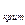при доверительной вероятности p = 0.90. Если 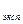Q>Q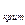выпадающий результат является промахом и его отбрасывают; при 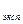Q<Q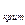результат не отбрасывают.

При обработке данных рассчитывают следующие основные характеристики выборочной совокупности.

Среднее для выборки из n результатов: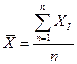

Дисперсию, характеризующую рассеяние результатов относительно среднего: 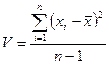n-1=f – число степеней свободы

Стандартное отклонение: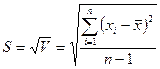

Относительное стандартное отклонение: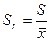

Дисперсия, стандартное отклонение и относительное стандартное отклонение – характеризуют воспроизводимость результатов химического анализа.

Доверительный интервал измеряемой величины для заданной доверительной вероятности (при отсутствии систематических погрешностей в этом интервале с соответствующей вероятностью находится истинное значени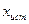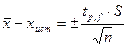е ): , где 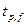- распределение Стьюдента;

S – стандартное отклонение измеряемой величины, рассчитанное для выборочной совокупности из n данных, а f = n – 1.

Доверительную вероятность P обычно принимают равной 0,95, хотя в зависимости от характера решаемой задачи ее можно полагать равной 0,90, 0,99 или какой-либо другой величине (табл.).Если известно истинное значение 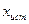, то доверительный интервал 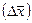характеризует как воспроизводимость результатов химического анализа, так и их правильность.

Обработанные данные можно представить в виде таблиц

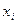
	n

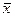
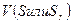
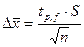
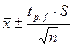
С применением методов математической статистики можно не только оценить результаты и случайные погрешности единичной серии результатов химического анализа, но сравнить данные двух совокупностей. Это могут быть результаты анализа одного и того же объекта, полученные двумя разными методами, в двух разных лабораториях, полученные различными аналитиками.

Сравнение двух дисперсий проводится при помощи F – распределения (распределения Фишера). Если имеются две выборочные совокупности с дисперсиям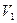и и 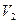и числами степеней свободы 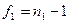и 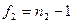соответственно, то значение 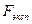рассчитывают по формуле: 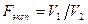при >.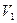

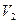Полученное значение сравнивают с табличным значением F – распределения. Если 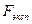>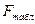при выбранной доверительной вероятности (обычно p= 0,05), то расхождение между дисперсиями значимо и рассматриваемые выборочные совокупности различаются по воспроизводимости. Если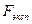 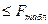, то различия в дисперсии имеет случайный характер.

Рассмотрим примеры.

Дата добавления: 2014-01-15