Баланс мощностей

Электрическая мощность в комплексном изображении.

Для вычисления активной, реактивной и полной мощностей цепи и ее участков необходимо знать действующие значения U, I и сдвиг фаз между ними φ = ψ_и – ψ_i.

Кроме того, для вычисления комплексной полной мощности необходимо перемножить комплексное напряжение на сопряженный комплексный ток

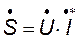. (8.15)

Сопряженным комплексным током 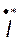называется зеркальное отображение комплексного тока 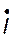относительно оси действительных чисел, что проиллюстрировано на рис. 8.5.

Если комплексный ток задан в алгебраической форме записи, то для получения сопряженного тока необходимо изменить знак на обратный перед мнимой частью его алгебраической формы записи. Если комплексный ток записан в показательной форме, то для получения сопряженного тока следует изменить знак на обратный перед его аргументом.

Таким образом: если 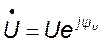, а , то полная мощность получится, как

. (8.16)

Используя тригонометрическую форму записи, можно из показательного выражения (8.16), перейти к алгебраической форме:

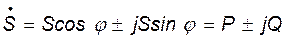. (8.17)

Вещественная часть Р выражения (8.17) равна активной мощности, а коэффициент Q при мнимой части равен реактивной мощности, причем при активно-индуктивном характере сопротивления цепи берется + Q, а при активно-емкостном – берется – Q.

Баланс мощностей в цепи синусоидального тока составляется раздельно для активной Р и реактивной Q мощностей, то есть для составления уравнения баланса мощностей необходимо определить комплексную полную мощность генераторов

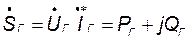и комплексные полные мощности, потребляемые элементами цепи, например, для q - ого элемента цепи:

.

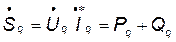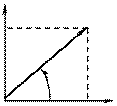
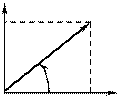
Векторная форма записи комплексного числа (8.17) проиллюстрирована на рис. 8.6, а в виде прямоугольного треугольника мощностей, который подобен прямоугольному треугольнику сопротивлений той же цепи (рис. 8.6, б).

		Рис. 8.6. Треугольники мощностей (а) и сопротивлений (б) электрической цепи

Im Iт Q x Z а) б) φ φ 0 Re 0 Re P r

Активная, реактивная, полная и комплексная мощности имеют одинаковую размерность [Дж/с]. Однако, для подчеркивания физических различий этих понятий, активная и мгновенная мощность выражается в ваттах [Вт], полная и комплексная мощности – а вольт-амперах [В•А], а реактивная мощность – в вольт-амперах реактивных [вар].

Для обеспечения передачи максимальной активной мощности в нагрузку при заданных действующих значениях токов и напряжений, как следует из выражения (8.17), необходимо увеличивать cosφ, то есть уменьшать сдвиг фаз между током и напряжением.

Величина , характеризующая степень приближения активной мощности нагрузки к максимальному значению, называется коэффициентом мощности.

При чисто резистивном характере нагрузки коэффициент мощности имеет максимальное значение cosφ = 1.

Комплексное сопротивление большинства реальных приемников энергии (электродвигателей, электронагревательных и осветительных приборов) имеет резистивно-индуктивный характер.

Для компенсации мнимой составляющей проводимости нагрузки параллельно ей должны подключаться компенсирующие конденсаторы.

Таким образом, рассмотрены R, L, С элементы и законы Ома и Кирхгофа в комплексном изображении, а также электрическая мощность в комплексном изображении, приведен баланс мощностей.

Тест 16

Дата добавления: 2014-01-15