Резонансная частота и добротность последовательного колебательного контура

Лекция 11. Резонансные явления в колебательном контуре

Воздействии

Тема 3. Резонансный контур при гармоническом

Комплексные частотные характеристики электрической цепи

Для каждого п. 1- 6 теста запишите номера только соответствующих ему позиций

Комплексная частотная характеристика	Воздействие	Выходная величина	Ед. измерения	Влияние на комплексную частотную характеристику …
внутренних элементов цепи	вида схемы соединения элементов цепи
1.Комплексное входное сопротивление. 2.Комплексная входная проводимость. 3. Комплексный коэффициент передачи по напряжению. 4. Комплексный коэффициент передачи по току. 5.Комплексное передаточное сопротивление. 6. Комплексная передаточная проводимость.	7. Только ток.   8. Только напряжение.	9. Только напряжение.   10. Только ток.   11. Нет	12. Ом   13. Сименс   14. Безразмерная	21. Да   22. Нет	23. Нет   24. Да

При последовательном соединении реактивных элементов, имеющих индуктивное и емкостное сопротивления (рис. 11.1), возможно явление резонанса напряжения, при котором разность фаз напряжения на крайних зажимах цепи и тока, протекающего по этой цепи, равна нулю.

Из рис. 11.1 следует, что ток, отдаваемый источником энергии е, называют током контура i; напряжение, создаваемое источником на зажимах 1- 2, обозначают напряжением контура и.

		Рис. 11. 1. Электрическая схема последовательного резонансного контура

Под входным сопротивлением Z резонансного контура понимается комплексное сопротивление последовательной RLC – цепи относительно крайних зажимов 1- 2

. (11.1)

Мнимая составляющая комплексного сопротивления (11.1) последовательного колебательного контура (рис. 11.1)

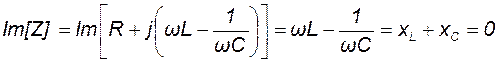(11.2)

должна быть равна нулю, когда угловая частота внешнего гармонического воздействия ω равна резонансной частоте контура ω₀. Полагая в выражении (11.2) ω = ω₀, получаем уравнение для нахождения резонансной частоты последовательного колебательного контура:

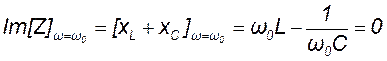, (11.3)

где 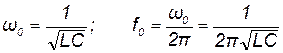. (11.4)

На резонансной частоте сопротивление емкостиравно сопротивлению индуктивности

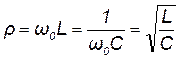. (11.5)

Величину ρ называют характеристическим сопротивлением контура. Как следует из выражения (11.5) значение ρ не зависит от частоты и определяется только параметрами реактивных элементов контура.

На резонансной частоте входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура

.

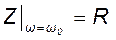Амплитуда тока контура на резонансной частоте

, (11.6)

где U_m - амплитуда напряжения на контуре.

Амплитуды напряжений на реактивных элементах контура на резонансной частоте определяются как:

.

Добротность – количественная мера степени приближения свойств реальных элементов к свойствам идеализированных элементов и определяется как модуль тангенса сдвига фаз между током и напряжением на зажимах соответствующего элемента:

.

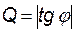Добротность индуктивной катушки: ,

а добротность конденсатора: .

Добротность последовательного контура характеризуется величиной отношений:

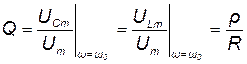. (11.7)

Используя выражение (11.5), добротность колебательного контура Q можно выразить через параметры его элементов:

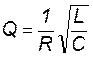. (11.8)

Как правило, добротность колебательных контуров современной радиотехнической аппаратуры лежит в пределах от нескольких десятков до нескольких сотен.

Добротность последовательного контура не может превышать добротности его элементов на резонансной частоте.

Как правило, Q_C >> Q_L, поэтому добротность последовательного контура в основном определяется добротностью индуктивной катушки на резонансной частоте.

После рассмотрения последовательного колебательного контура остановим внимание на параллельном резонансном колебательном контуре.

Дата добавления: 2014-01-15