
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Избирательные свойства колебательного контура
|
|
|
|
Если на вход колебательного контура подать сумму гармонических колебаний различных частот, имеющих одинаковые амплитуды, то на выходе можно обнаружить, что амплитуда колебаний, частота которых близка к резонансной, значительно превышает амплитуды колебаний, частоты которых существенно отличаются от резонансной.
Способность электрической цепи выделять колебания отдельных частот из суммы колебаний различных частот называется избирательностью.
В идеальном случае отклик избирательной цепи должен иметь постоянное значение в пределах определенного диапазона частот, называемого полосой пропускания цепи, и быть равным нулю за пределами этого диапазона.
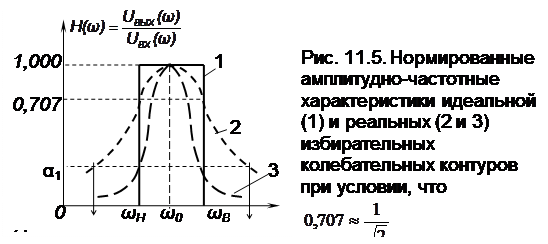
Нормированная амплитудно-частотная характеристика идеальной избирательной цепи должна иметь прямоугольную форму (кривая 1 на рис. 11.5). Амплитудно-частотная характеристика реальных избирательных цепей, в том числе и амплитудно-частотная характеристика последовательного колебательного контура (кривая 2 на рис. 11.5), отличается от прямоугольной отсутствием резкой границы между диапазонами пропускаемых и задерживаемых (подавляемых) частот.
Как видно из рис. 11.5 (кривые 2 и 3) избирательные свойства реальных колебательных контуров тем выше, чем ближе к прямоугольной форма их нормированной амплитудно-частотной характеристики.
 |
Избирательные свойства оцениваются коэффициентом прямоугольности и шириной полосы пропускания.
Коэффициент прямоугольности амплитудно-частотной характеристики находится как отношение значений полосы пропускания, измеренных на уровнях α1 и α2:
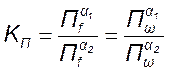 при α2 > α1. (11.18)
при α2 > α1. (11.18)
Полоса пропускания (ширина полосы пропускания) реальных избирательных устройств определяется на уровне α = 0,707 от максимального значения
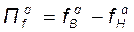 или
или 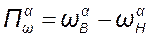
Оценим избирательные свойства последовательного колебательного контура, рассматривая его амплитудно-частотную характеристику проводимости (рис. 11.6) 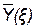 , которая была построена с помощью выражений:
, которая была построена с помощью выражений:
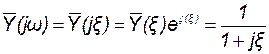 ;
;
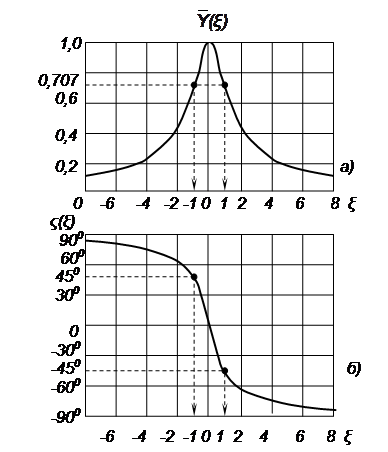 | |||
| |||
;
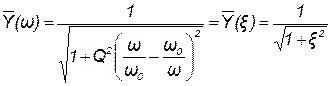 ;
;
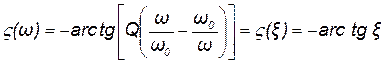
Из рис. 11.6, а следует, что на границах полосы пропускания на уровне 0,707 абсолютное значение обобщенной расстройки равно единице, а аргумент входной проводимости последовательного контура (рис. 11.6, б) равен 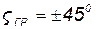 .
.
Полоса пропускания последовательного колебательного контура обратно пропорциональна его добротности, не зависит от ёмкости С и на уровне 0,707 в Q раз меньше значения его резонансной частоты.
Что касается коэффициента прямоугольности амплитудно-частотной характеристики последовательного колебательного контура, то его значение, измеренное по ширине полосы пропускания на уровнях 0,707 и 1/100, составляет
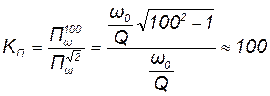 .
.
Следовательно, коэффициент прямоугольности амплитудно-частотной характеристики последовательного колебательного контура оказывается намного больше единицы, что свидетельствует о том, что его избирательные свойства далеки от свойств идеальной избирательной цепи.
В связи с тем, что нормированные передаточные характеристики последовательного и параллельного колебательных контуров совпадают, их избирательные свойства одинаковы.
Таким образом, были рассмотрены резонансные явления и частотные характеристики колебательных параллельного и последовательного контуров, а также их избирательные свойства.
Тест 22
Резонанс колебательных RLC контуров
Для каждого п. 1 и 2 теста запишите номера только соответствующих ему позиций
| Колебательный контур | Условие резонанса: мнимое сопротивление контура равно нулю | Резонансная частота ω | Действующее значение | |||
| токов | напряжений | |||||
| емкости | индуктивности | ёмкости | индуктивности | |||
| 1. Последовательный. 2. Параллельный. | 3. 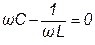 4.
4. 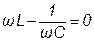
| 5.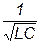 6.
6.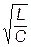
| 7. Равно току индуктивности. 8. Равно току потерь | 9. Равно току потерь. 10. Равно току ёмкости | 11. Равно напряжению потерь. 12. Равно напряжению индуктивности. | 13. Равно напряжению ёмкости. 14. Равно напряжению потерь. |
Тест 23
|
|
|
Дата добавления: 2014-01-15; Просмотров: 6942; Нарушение авторских прав?; Мы поможем в написании вашей работы!