Диаграммы нулей и полюсов

Определение частотных характеристик цепи с помощью

Построение амплитудно-частотной и фазовой частотной характеристик цепи с помощью диаграмм нулей и полюсов передаточной функции цепи начнем для случая, когда все полюсы и нули Н_kν(p) располагаются на действительной оси комплексной плоскости частоты .

Если все полюсы и нули находятся на оси σ, то согласно методу Г. Боде [3] можно записать

(14.4)

где К, а, b, c, d, … - действительные константы.

Положим на время, что при р = 0 нет ни полюсов, ни нулей. Тогда выражение (14.4) удобно записать в виде

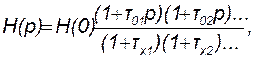(14.5)

где τ_0i и τ_хi – постоянные времени, соответствующие нулю и полюсу передаточной функции (14.1).

Прологарифмировав выражение (14.5) и заменив р = jω, получим значение функции (модуля)

(14.6)

и аргумента

(14.7)

исследуемой передаточной функции (14.1) цепи.

Зная амплитудную и фазовую характеристики всех отдельных членов выражений (14.6) и (14.7), легко с помощью простого суммирования получить амплитудно-частотную и фазовую частотную характеристики всей исследуемой передаточной функции (14.1) цепи в целом.

Амплитудно-частотная и фазовая частотная характеристики любого слагаемого выражений (14.6) и (14.7) имеют вид, показанный на рис. 14.4.

Графические зависимости, проиллюстрированные на рис. 14.4, имеют логарифмический масштаб изменения оси частот и прямолинейные асимптоты.

Точка излома характеристик располагается на частоте

или .

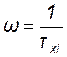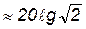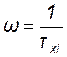Отклонения кривой логарифмической амплитудной частотной характеристики от асимптот составляет примерно 3 дБ () на частоте излома или . Отклонения графика логарифмической фазовой частотной характеристики от асимптоты не превышают 6⁰.

Из рассмотрения рис. 14.4 следует, что наклон асимптоты логарифмической амплитудно-частотной характеристики равен 20 дБ амплитуды на одну декаду частоты.

Рассмотрим диаграмму полюсов – нулей передаточной функции параллельного колебательного контура, схема которого приведена на рис. 14.5

Передаточная функция входного сопротивления параллельного резонансного контура (рис. 14.5) имеет вид

(14.8)

где - резонансная частота;

- добротность колебательного контура.

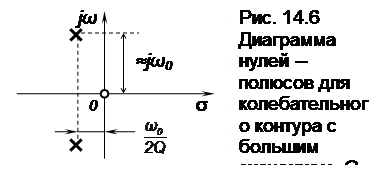
Резонанс заслуживает внимание главным образом, когда добротность Q колебательного контура велика, например, при Q > 10. При этом полюсы в виде комплексно-сопряженных чисел (рис. 14.6) передаточной функции (14.8) колебательного контура будут находиться достаточно близко к оси jω комплексной плоскости частот.

В этом случае амплитудно-частотная характеристика колебательного контура имеет вид

(14.9)

где К = R;

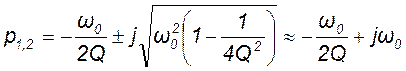- полюсы передаточной функции (14.9) колебательного контура, изображенного на рис. 14.5.

Для аппроксимации H(jω) вблизи резонансной частоты ω ≈ ω₀ мы можем считать, что векторы (jω ─ 0) и (jω – p₂) являются по существу постоянными, не зависящими от ω, и равными соответственно jω₀ и 2 jω₀.

Тогда поведение H(jω) определяется быстрым изменением вектора (jω – p₁) при ω ≈ ω₀:

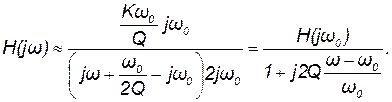(14.10)

При или 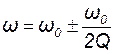мы имеем

.

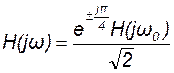Таким образом, были рассмотрены диаграммы нулей и полюсов передаточной функции цепи и методика определения частотных характеристик цепи с помощью этих диаграмм нулей и полюсов.

Тест 32

Дата добавления: 2014-01-15