Амплитудно-модулированный сигнал

Математическую модель амплитудно-модулированного сигнала можно представить в виде

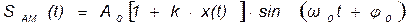(16.2)

или ,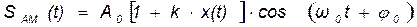

где 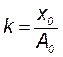- коэффициент глубины амплитудной модуляции;

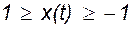- пределы изменения модулирующего сигнала;

А₀ – амплитуда несущего колебания;

х₀ = 1 – амплитуда модулирующего колебания;

ω₀ = const – частота несущего колебания;

φ₀ = const – начальная фаза колебания несущей.

На рис. 16.1 приведены осциллограммы амплитудно-модули рованного сигнала с разной глубиной модуляции.

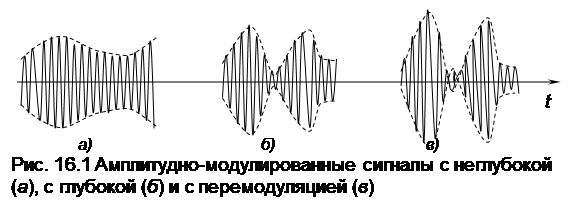Из рассмотрения рис. 16, в следует, при перемодуляции, когда k > 1, происходит потеря повторения формы модулирующего сигнала.

В случае, когда модулирующим низкочастотным сигналом является гармоническое колебание с частотой Ω, то амплитудно-модулированный сигнал называется однотональным и его математическая модель имеет вид

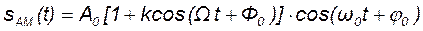. (16.3)

Из выражения (16.3) с учетом тригонометрической формулы произведения косинусов получаем

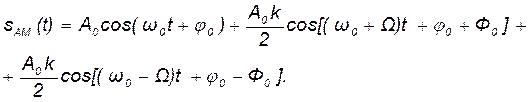(16.4)

В выражении (16.4) слагаемыми являются:

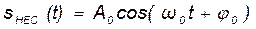─ (16.5)

─ несущая составляющая колебания;

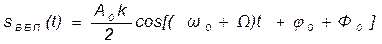─ (16.6)

─ составляющая верхней боковой полосы частотного спектра амплитудно-модулированного сигнала;

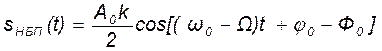─ (16.7)

─ составляющая нижней боковой полосы частотного спектра амплитудно-модулированного сигнала.

Анализ выражений (16.5), (16.6) и (16.7) показывает на равенство амплитуд верхнего и нижнего боковых колебаний, а также на симметрию расположения этих спектральных составляющих относительно несущего колебания (16.5).

Средняя мощность амплитудно-модулированного колебания равна сумме двух слагаемых:

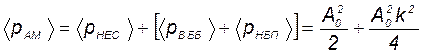. (16.8)

Из выражения (16.8) видно, что даже при 100% модуляции (k = 1) доля мощности обоих боковых колебаний составляет всего лишь 50% от мощности немодулированного несущего колебания. Поскольку информацию о сообщении несущая не несет, информация об этом сообщении заключена в боковых колебаниях, то можно отметить неэффективное использование мощности амплитудно-модулированного сигнала.

Поэтому на практике амплитудно-модулированные сигналы передают с помощью одной или двух одновременно боковых полос частотного спектра, подавляя несущую составляющую.

Международная классификация типов (видов) сигналов предусматривает обозначение амплитудно-модулированного сигнала индексом: А3, с использованием одной только верхней боковой полосы частотного спектра (однополосная амплитудная модуляция): А3В; - нижней боковой полосы: А3Н; - с подавленной несущей: А3J.

Дата добавления: 2014-01-15