Минимизация булевых функций с помощью карт Карно

Для минимизации функций относительно небольшого числа переменных (не более шести) наиболее простым и наглядным является графический метод, использующий карты Карно.

Карта Карно – это прямоугольник, разбитый на квадраты, число которых равно числу наборов рассматриваемой функции, т. е. 2 ⁿ. Клетки размечаются так, чтобы наборы, для которых возможны смежные конституенты, оказались бы в соседних клетках.

При заполнении карты Карно в ее клетки проставляют значения функции для соответствующих наборов, которые являются координатами клеток. Например, для функции двух переменных А и В (рис. 2.4) карта Карно имеет вид:

Номер набора	А	В	F		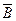	B		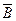	B
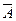
					№ 0	№ 1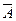
				A	№ 2	№ 3	A
3

Рис. 2.4. Карта Карно для булевой функции двух переменных

Единицы, представленные в клетках, обозначают конституенты единицы рассматриваемой функции. Отыскание минимальной ее формы сводится к определению варианта, при котором все конституенты единицы накрываются (охватываются контурами покрытия) наименьшим числом наиболее коротких импликант. Объединение клеток на карте эквивалентно выполнению операции склеивания.

Всегда нужно стремиться к минимальному количеству контуров и максимальной площади каждого из них, руководствуясь следующими правилами:

· площадь контура покрытия должна быть S_k = 2 ^{m - i} клеток, где – целое число, m – число переменных. Если, например, m = 3, то S_k = 1, 2, 4, или 8 клеток;

· число сокращаемых переменных N _перем.= log₂ S_k, т.е. при S_k = 1 не сокращается ни одна переменная, при S_k = 2 сокращается одна переменная и т.д.

В примере на рис. 2.4 пара единиц верхней строки охватывается импликантой Ā, т.е. обе клетки имеют общий аргумент Ā. Пара единиц правого столбца накрывается импликантой B, как общей для обеих клеток. Следовательно, минимальная ДНФ функции F (A, B) = Ā Ú B.

Если имеется несколько вариантов объединения конституент контурами, то можно получить несколько различных эквивалентных минимальных ДНФ функции, одна из которых выбирается для реализации в цифровом устройстве.

Карту Карно удобно использовать и для минимизации функций, заданных в алгебраической форме, например,

.

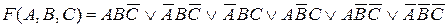Карта Карно, состоящая из 2³ = 8 клеток, может быть размечена, как показано на рис. 2.5.

При охвате единиц контурами склеивания карту Карно можно сворачивать в цилиндр, как вдоль горизон-тальной, так и вертикальной оси. В результате все четыре единицы, расположенные в углах Карты, охватываются контуром с общей импликан-той . Такой минимизации соответствует выражение

.

Минимизация недоопределенных функций

Недоопределенность функции предполагает, что запрещенные наборы никогда не появятся в процессе работы устройства. Значит, такую функцию можно произвольно доопределить, установив ее значения на запрещенных наборах. Это не отразится на работе устройства, но может упростить его реализацию.

Пусть необходимо минимизировать булеву функцию, заданную картой Карно (рис. 2.6).

Если группировать единицы в контурах только по исходному заданию (рис. 2.6, а), то минимальная форма функции будет иметь вид:

.

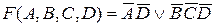		B	A				B	A
			–
D			–			D
C			–	–		C
		–	–

а б

Рис.2.6. Минимизация недоопределенной функции

После доопределения функции (рис. 2.6, б), ее минимальная ДНФ (заметим, что это будет уже другая полностью определенная функция j) оказывается предельно простой

.

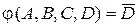Функция j, значения которой совпадают со значениями заданной функции F на тех наборах, где F определена, называется эквивалентной. Таким образом, задача минимизации недоопределенной функции сводится к отысканию такой эквивалентной функции, которая имеет простейшую форму. При синтезе комбинационных схем всегда возникает вопрос выявления опасных состязаний, которые по характеру перехода устройства от одного состояния к другому разделяются на статические и динамические состязания. Статические состязания имеют место в случае, когда по алгоритму функционирования для двух соседних состояний значение логической функции остается неизменным. Динамические состязания могут возникнуть при формировании соседними входными состояниями алгоритмического перехода от нуля к единице или наоборот на выходе устройства. На практике большее внимание уделяют статическим состязаниям, с этой целью пользуются простым и удобным формальным критерием Хаффмена: статические опасные состязания в устройстве с минимизированной структурой могут иметь место, если на карте Карно при охвате соседних клеток контурами склеивания окажутся хотя бы две соседние клетки, не покрытые контуром.

Поэтому устранение опасных состязаний достигается возвращением импликант, которые оказались лишними при переходе от сокращенной к тупиковой ДНФ.

2.6. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
НА ЭЛЕМЕНТАХ И–НЕ, ИЛИ–НЕ

При реализации цифровых устройств стремятся сузить номенклатуру применяемых интегральных микросхем за счет использования только функционально полного базиса И-НЕ или только базиса ИЛИ-НЕ. Для этого минимизированные логические функции путем преобразований приводятся к соответствующему виду.

Пусть задана минимальная ДНФ функция вида:

.

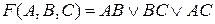Применим к этому выражению двойное отрицание и теорему де Моргана

.

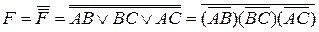Как видно, после преобразования функция F включает только операции И-НЕ, и ее реализация в базисе И-НЕ имеет вид (рис. 2.7)

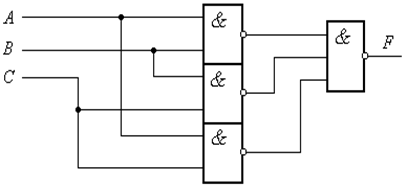
Рис. 2.7. Реализация функции в базисе И-НЕ

Аналогичным образом от КНФ функции можно перейти к ее форме, удобной для реализации в базисе ИЛИ-НЕ.

3. ЭЛЕМЕНТНАЯ БАЗА ЦИФРОВЫХ СИСТЕМ

3.1. ПРИНЦИПЫ ПОСТРОЕНИЯ
ПОЛУПРОВОДНИКОВЫХ КЛЮЧЕВЫХ СХЕМ

В цифровой электронике ключевая схема предназначена для коммутации (переключения) тока в нагрузке и создания двух резко отличающихся уровней (перепадов) напряжения на нагрузке, соответствующих логическому нулю и логической единице.

Ключевая схема на биполярном транзисторе

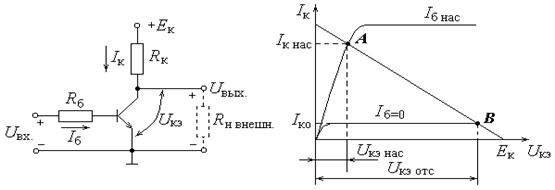
В интегральных микросхемах выполненных на биполярных транзисторах роль ключа выполняет транзистор, включенный по схеме с общим эмиттером (рис. 3.1).

а б

Рис.3.1. Ключевая схема на биполярном транзисторе: а - принципиальная схема; б – вольт/амперная характеристика ключа

Управление состоянием ключа осуществляется сигналом U _вх. При U _вх = 0, соответственно I _б = 0 и состояние схемы определяется точкой B на вольт-амперной характеристике (ВАХ) ключа. Транзистор находится в состоянии отсечки, что эквивалентно разомкнутому ключу, а выходное напряжение U _вых равно U _{кэ отс}, т. е. несколько меньше, чем E _к. Ток через транзистор I _ко в этом случае пренебрежительно мал.

При U _вх, достаточном для создания базового тока I _{б нас}, переводящего транзистор в режим насыщения, состояние схемы определяется точкой А на ВАХ, что равносильно замкнутому ключу. Выходное напряжение равно U _{кэ нас}, т.е. несколько выше нулевого уровня, а ток через транзистор I _{к нас} максимален и равен .

Оценим энергетические затраты в ключевой схеме:

1. В режиме отсечки мощность, выделяемая на транзисторе и вызывающая его нагревание, определяется выражением

P _отс = I _ко × U _{кэ отс} .

Вследствие крайней малости I _ко, мощность P _отс значительно меньше допустимой величины.

2. В режиме насыщения мощность P _нас = I _{к нас} × U _{кэ нас}. Так как U _{кэ нас} мало, P _нас также находится в допустимых пределах.

3. Более подробно рассмотрим процесс переключения – процесс перехода ключа из одного состояния в другое.

В течение времени переключения t_ф, ток i _к(t) и напряжение U _кэ(t) достигают относительно высоких величин. На переключение транзистора затрачивается энергия

Допустив, что ток i _к(t) за время переключения изменяется по линейному закону, т.е. i _к(t) = I _нас × t/ t_ф, и, считая, что R _к, E _к известны, получим

.

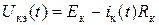Тогда с учетом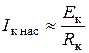

.

Если транзистор ключа переключается с частотой f, то мощность,

выделяемая на нем, будет равна

,

где – период переключения.

Режим переключения является наиболее энергоемким режимом работы транзисторного ключа. В этом случае, по мере увеличения частоты переключения, P _{перекл.} может достигать значительных величин. Это приводит к необходимости принятия дополнительных мер по обеспечению нормального теплово-го режима в цифровых схемах.
Идеализированная временная диаграмма (без учета переходных процессов) работы ключа приведена на рис. 3.2. Ее анализ показывает, что для статического режима, если U _вх – низкий потенциал, то U _вых – высокий, и наоборот. Следователь-но, простейшая ключевая схема на транзисторе с нагрузкой в цепи коллектора, с которого снимается выходное напряжение, является инвертором, реализующим функцию НЕ как в положительной, так и в отрицательной логике.

Ключевая схема на полевых транзисторах

Ключевые схемы на полевых (МДП) транзисторах имеют следующие преимущества перед биполярными:

· малое сопротивление в открытом состоянии,

· высокое сопротивление в закрытом состоянии,

· малая потребляемая мощность при высокой помехоустойчивости и нагрузочной способности,

· широкий диапазон питающих напряжений.

Нагрузкой в таком ключе может служить линейный резистор, однако в интегральной схемотехнике в качестве нагрузочного резис-

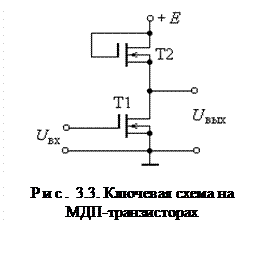тора R используется МДП-транзистор того же типа, что и транзистор, выполняющий роль ключа (рис. 3.3). Это позволяет сократить число технологических операций при изготовлении микросхем. Чтобы транзистор Т2 выполнял роль резистора необходимо обеспечить постоянно открытое состояние его канала. Для этого затвор транзистора Т2 соединяют с его стоком.

Ключевая схема на комплементарных транзисторах

В рассмотренных ключевых схемах существенным недостатком является протекание тока через сопротивление R _к как в открытом, так и в закрытом состояниях ключа и, как следствие, его значительное нагревание.

Этого недостатка лишен инвертор на комплементарных (взаимодополняющихся) МДП-транзисто-рах (рис. 3.4). Схема построена на двух транзисторах Т1 и Т2 с одинаковыми характеристиками, но с каналами разных типов прово-димости. Схема симметрична: ког-да один из транзисторов выполня-ет роль замкнутого ключа, то дру-гой служит нагрузочным сопротивлением и наоборот.

В положительной логике и при положительной полярности напряжения питания при подаче на вход схемы логического 0 (U _вх» 0 В) транзистор Т1 будет заперт, а транзистор Т2 оказывается в режиме глубокого насыщения и через него потенциал + Е поступает на выход, реализуя на выходе логическую 1. Сквозной ток, протекающий через оба последовательно соединенных транзистора, практически равен нулю, так как сопротивление закрытого транзистора Т1 очень велико.

Если на вход ключа подана логическая 1, то состояния транзисторов меняются на противоположные и через открытый транзистор Т1 на выход будет подан нулевой потенциал корпуса U _вых» 0 В, реализуя логический 0. При этом сквозной ток по прежнему останется близким к нулю вследствие большого сопротивления запертого транзистора Т2.

Таким образом, в статическом состоянии схема практически не потребляет мощности от источника питания.

В режиме переключения имеется некоторый интервал времени в течение которого открыты оба транзистора и поэтому сквозной ток может достигать значительных величин. Однако для КМДП-ключей типичны низкие напряжения питания, так что заметного возрастания тока во время переключения обычно не происходит.

Дата добавления: 2014-01-15