
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Настройка весовых векторов Вj
|
|
|
|
Выражение, описывающее процесс настройки весов (выражение (8.6) повторено здесь для справки) является центральным для описания процесса функционирования сетей APT.
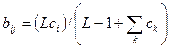
Сумма в знаменателе представляет собой количество единиц на выходе слоя сравнения. Эта величина может быть рассмотрена как «размер» этого вектора. В такой интерпретации «большие» векторы С производят более маленькие величины весов bij, чем «маленькие» вектора С. Это свойство самомасштабирования делает возможным разделение двух векторов в случае, когда один вектор является поднабором другого; т.е. когда набор единичных компонент одного вектора составляет подмножество единичных компонент другого. Чтобы продемонстрировать проблему, возникающую при отсутствии масштабирования, используемого в выражении (8.6), предположим, что сеть обучена двум приведенным ниже входным векторам, при этом каждому распределен нейрон в слое распознавания.
Х1 = 1 0 0 0 0
X2= 1 1 1 0 0
Заметим, что Х1 является поднабором Х2. В отсутствие свойства масштабирования веса bij и tij получат значения, идентичные значениям входных векторов. Если начальные значения выбраны равными 1,0, веса образов будут иметь следующие значения:
T1 = В1 = 1 0 0 0 0
Т2 = B2 =1 1 1 0 0
Если X прикладывается повторно, оба нейрона в слое распознавания получают одинаковые активации; следовательно, нейрон 2, ошибочный нейрон, выиграет конкуренцию. Кроме выполнения некорректной классификации, может быть нарушен процесс обучения. Так как Т2 равно 1 1 1 0 0, только первая единица соответствует единице входного вектора, и С устанавливается в 1 0 0 0 0, критерий сходства удовлетворяется и алгоритм обучения устанавливает вторую и третью единицы векторов Т2 и В2 в нуль, разрушая запомненный образ. Масштабирование весов bij предотвращает это нежелательное поведение. Предположим, что в выражении (8.2) используется значение L=2, тем самым определяя следующую формулу:

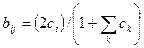
Значения векторов будут тогда стремиться к величинам
В1 = 1 0 0 0 0
В2 = 1/2 1/2 1/2 0 0
Подавая на вход сети вектор X1, получим возбуждающее воздействие 1,0 для нейрона 1 в слое распознавания и 1/2 для нейрона 2; таким образом, нейрон 1 (правильный) выиграет соревнование. Аналогично предъявление вектора Х2 вызовет уровень возбуждения 1,0 для нейрона 1 и 3/2 для нейрона 2, тем самым снова правильно выбирая победителя.
Инициализация весов bij
Инициализация весов bij малыми значениями является существенной для корректного функционирования систем APT. Если они слишком большие, входной вектор, который ранее был запомнен, будет скорее активизировать несвязанный нейрон, чем ранее обученный. Выражение (8.1), определяющее начальные значения весов, повторяется здесь для справки
bij < L / (L - 1+ т) для всех i, j. (8.1)
Установка этих весов в малые величины гарантирует, что несвязанные нейроны не будут получать возбуждения большего, чем обученные нейроны в слое распознавания. Используя предыдущий пример с L= 2, т=Ъ и bij < 1/3, произвольно установим bij = 1/6. С такими весами предъявление вектора, которому сеть была ранее обучена, приведет к более высокому уровню активации для правильно обученного нейрона в слое распознавания, чем для несвязанного нейрона. Например, для несвязанного нейрона Х будет производить возбуждение 1/6, в то время как Х будет производить возбуждение 1/2; и то и другое ниже возбуждения для обученных нейронов.
Поиск. Может показаться, что в описанных алгоритмах отсутствует необходимость наличия фазы поиска за исключением случая, когда для входного вектора должен быть распределен новый несвязанный нейрон. Это не совсем так; предъявление входного вектора, сходного, но не абсолютно идентичного одному из запомненных образов, может при первом испытании не обеспечить выбор нейрона слоя распознавания с уровнем сходства большим р, хотя такой нейрон будет существовать. Как и в предыдущем примере, предположим, что сеть обучается следующим двум векторам:
Х =1 0 0 0 0
X = 1 1 1 0 0
с векторами весов Вi, обученными следующим образом:
В1=1 0 0 0 0
В2 = 1/2 1/2 1/2 0 0
Теперь приложим входной вектор Х3 = 1 1 0 0 0. В этом случае возбуждение нейрона 1 в слое распознавания будет 1,0, а нейрона 2 только 2/3. Нейрон 1 выйдет победителем (хотя он не лучшим образом соответствует входному вектору), вектор С получит значение 1 1 0 0 0, S будет равно 1/2. Если уровень сходства установлен в 3/4, нейрон 1 будет заторможен и нейрон 2 выиграет состязание. С станет равным 1 1 0 0 0, S станет равным 1, критерий сходства будет удовлетворен и поиск закончится.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!