Принцип Гюйгенса-Френеля

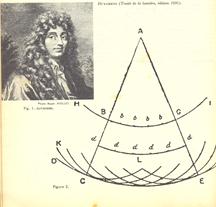Явление дифракции, то есть огибание волнами препятствий и проникновение их в область геометрической тени, качественно объяснил голландский астроном, механик и физик Христиан Гюйгенс. В трактате «Распространение света» (1678 г.) он впервые высказал идею о вторичных волнах. По Гюйгенсу, любая точка пространства, до которой дошёл фронт волны, становится элементарным источником вторичных сферических волн. Новое положение фронта волны совпадает с огибающей всех вторичных волн (рис. 7.4. Из трактата Х.Гюйгенса «Распространение света»).

Рис.7.4

Это довольно искусственное предположение Гюйгенса получило неожиданное развитие в работе французского инженера-строителя Жана Френеля. В 1819 году (вскоре после окончания франко-русской кампании) Френель опубликовал свою знаменитую работу «Экспериментальное и теоретическое исследование дифракционных явлений».

Суть френелевой теории дифракции состоит в следующем.

Для отыскания интенсивности колебаний, создаваемых источником в точке наблюдения P (рис. 7.5), окружим источник произвольной замкнутой поверхностью S.

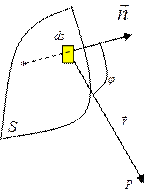
Рис. 7.5

В соответствии с принципом Гюйгенса, каждая точка этой поверхности должна рассматриваться как источник вторичных сферических волн.

Интенсивность в точке P можно отыскать, сложив бесконечное число вторичных волн, учитывая их амплитуду и фазу.

По Френелю каждый элемент поверхности dS излучает элементарную сферическую волну, которую в точке наблюдения P можно записать так

. (7.1)

Здесь: a ₀ — амплитуда вторичной волны на поверхности dS;

r — расстояние от поверхности до точки наблюдения P (вторичная волна – сферическая, поэтому её амплитуда убывает с расстоянием a ₀/ r),

k (φ) — коэффициент, зависящий от угла φ между нормалью к элементу dS и направлением на точку P. Этот коэффициент максимален при φ = 0 и равен 0 при .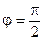

Амплитуда результирующего колебания равна

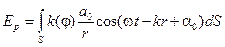. (7.2)

Теперь легко отыскать интенсивность волны в точке наблюдения P: ведь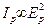

Ещё раз вкратце повторим суть теории дифракции Френеля.

Назовём реальный источник A — первичным источником, излучаемую им волну — первичной волной.

Выделенная замкнутая поверхность S представляет собой геометрическое место точек — вторичных источников. Они излучают вторичные волны.

Принцип Гюйгенса-Френеля предлагает заменить первичную волну реального источника в точке наблюдения P суперпозицией вторичных волн, излучаемых поверхностью S.

В результате сложения бесконечного числа волн в точке наблюдения может возникнуть как максимум, так и минимум интенсивности. Всё будет определяться соотношением фаз складываемых волн.

Почему же в таком случае это явление получило название «дифракция», а не «интерференция»?

Это исторически сложившаяся терминология: результат сложения нескольких когерентных волн – интерференция, суперпозиция N волн — многолучевая интерференция, а сумма бесконечного числа волн — уже дифракция.

Дата добавления: 2014-01-15