Интенсивность дифракционной картины

Вновь разделим поверхность щели на узкие полоски, параллельные её краям. Но теперь проследим за тем, чтобы все эти подзоны были одинаковой площади. В этом случае вторичные волны, излучаемые полосками, будут иметь одинаковые амплитуды Δ А.

Каждая следующая волна, кроме того, будет иметь неизменный сдвиг по фазе относительно предыдущей. Величина фазового сдвига будет зависеть от угла φ.

Сложим графически все эти волны в максимуме нулевого порядка (φ = 0). Здесь все волны собираются в фазе. Соответствующая векторная диаграмма приведена на рис. 8.4.

Рис. 8.4

Эта сумма равна А ₀. Особо отметим очевидный, но важный факт: амплитуда результирующего колебания А ₀ равна сумме модулей векторов .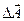

Обратимся теперь к направлению(φ₁), соответствующему первому максимуму.

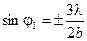
Этому направлению отвечает разность хода волн от краёв щели, равная :

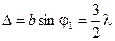
Это означает, что щель может быть поделена на 3 зоны Френеля. Две из них погасят друг друга, а третья обеспечит максимум номер 1 (первый дифракционный максимум).

Соответствующая векторная диаграмма (спираль) приведена на рис. 8.5.

Рис.8.5

Вспомним «очевидную, но важную деталь»: длина этой спирали – по-прежнему А ₀, т.е.

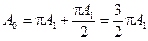
Следовательно, .

Вычислим амплитуду второго максимума. Его условие:

Спираль, отвечающая первому максимуму, имела полтора витка (см. рис. 8.5).

А теперь подобная же векторная диаграмма будет иметь уже два с половиной витка (при той же длине А ₀!)

Значит, полная длина спирали в два с половиной оборота будет равна

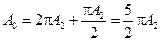
Таким образом, во втором максимуме амплитуда колебания составит такую величину:

Итак,

,

Легко догадаться, не производя вычислений, что в третьем максимуме амплитуда

,

затем

.

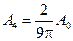И так далее.

Интенсивности колебаний в максимумах будут соотноситься как квадраты амплитуд, то есть: , ,

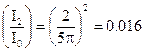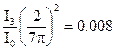
С увеличением номера максимума интенсивность быстро уменьшается, то есть основная энергия, прошедшая с волной сквозь щель, локализуется в «нулевом» центральном максимуме (рис. 8.3).

Вычислим теперь угловую ширину центрального максимума (см. рис. 8.3). Он ограничен первыми минимумами, условия которых известны:

.

Отсюда угловая ширина нулевого максимума

.

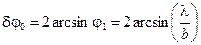При малом угле , поэтому

.

Дата добавления: 2014-01-15