Закон Гука при кручении

Деформации и напряжения при кручении.

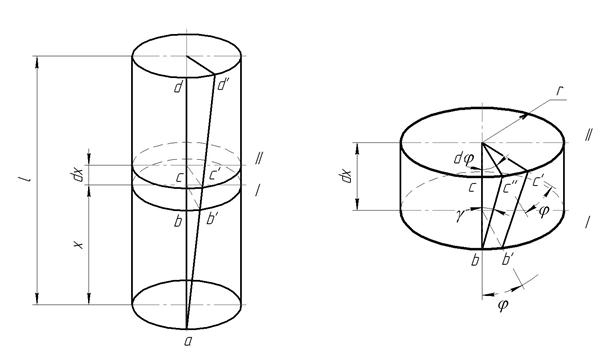
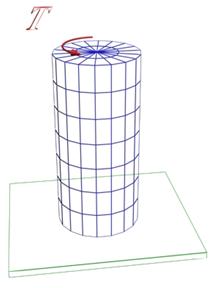Рассмотрим цилиндр, один конец которого закреплён неподвижно, а к другому приложен крутящий момент.

Образующая ad займёт положение 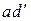. На расстоянии x выделим элемент dx. И получим точки 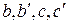. В элементе dx сечение I повернётся относительно основания на угол φ, а сечение II на угол φ+dφ.

γ – угол сдвига.

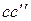- абсолютный сдвиг.

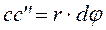
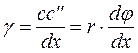
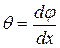- относительный угол закручивания.

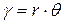(1).

Для цилиндров постоянного сечения и постоянно действующего крутящего момента можно утверждать, что для каждого элементарного участка dF, находящегося на радиусе r от центра сечения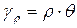

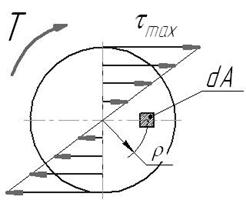
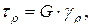- 1-я форма записи закона Гука.

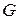- модуль упругости 2-го рода.

.

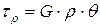Из эпюры видно, что максимальные касательные напряжения τ действуют на поверхности цилиндра, а в центре равны 0, поэтому валы, работающие на кручение, можно изготавливать полыми.

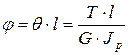- 2-я форма записи закона Гука при кручении.

,

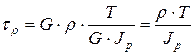
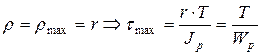где 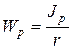- полярный момент сопротивления сечения.

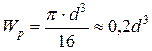- полярный момент сопротивления сечения (для круглого сечения).

7. Расчёты на прочность деталей, работающих в условиях сложного нагружения.

В различных механизмах детали работают не только на растяжение или изгиб или на кручение. Отдельные детали, как правило, испытывают воздействие нескольких нагрузок одновременно.

Следовательно, они находятся в условиях сложного нагружения.

В таких случаях расчёты производят с учётом гипотезы независимости действия сил, т.е. определяют напряжение от воздействия каждого силового фактора и затем определенным образом суммируют по одной из теорий прочности.

C:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.aviC:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.aviC:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.avi 7.1. Изгиб с кручением.

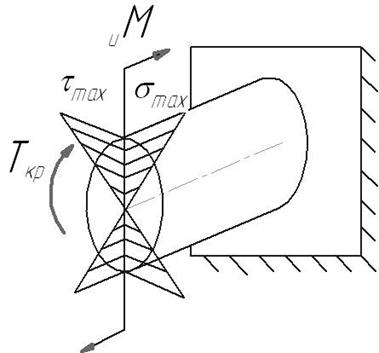C:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.aviC:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.aviC:Сопромат_2010Сложн_СопротВидеоЗуб_передач_Раб.aviИзгиб с кручением - этот вид нагружения, наиболее часто встречающийся в валах зубчатых передач.

- 3-я теория прочности.

;

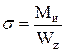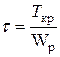
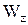- осевой момент сопротивления сечения;

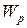- полярный момент сопротивления сечения.

,

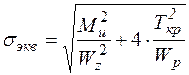Для сплошного вала круглого сечения

.

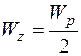Тогда:

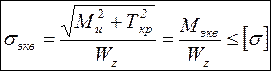- условие прочности при совместном действии изгиба и кручения.

8. Устойчивость сжатых стержней.

Если на стержень, закреплённый определённым образом воздействовать вертикальной продольной силой, то до определенной нагрузки P_кр стержень будет сохранять форму.

Система находится в деформированном состоянии равновесия между внешними нагрузками и вызываемыми ими силами упругости. Это состояние может быть устойчивым и не устойчивым.

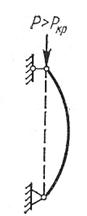
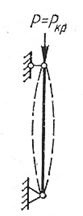
I II III

I – устойчивая форма равновесия P<P_кр.

Деформированное тело при любом малом отклонении от положения равновесия (поперечной силой F) стремится вернуться к первоначальному состоянию после снятия нагрузки.

II – потеря устойчивости P>P_кр.

При любом малом отклонении от состояния равновесия тело деформируется и после снятия нагрузки либо не возвращается в исходное состояние, либо может потерять равновесие.

III – состояние безразличного равновесия P=P_кр,, при любом малом отклонении тело может сохранить исходную форму или может потерять равновесие.

Достижение нагрузками критических значений равносильно разрушению конструкций, следовательно, для обеспечения устойчивости необходимо выполнить условие

,

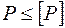где 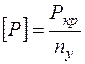- допускаемая продольная сила;

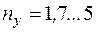- коэффициент запаса устойчивости.

Для определения критической силы используем формулу Эйлера:

_,

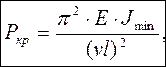где J_min - минимальный осевой момент инерции сечения;

Е – модуль упругости при растяжении (сжатии);

n - коэффициент закрепления концов стержня.

Дата добавления: 2014-01-15