
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Марківський випадковий процес і ланцюги Маркова
|
|
|
|
Марківський процес − це випадковий процес, що базується на принципі Маркова. Згідно з цим принципом ймовірність значень випадкової величини у наступні моменти  не залежать від того, які значення вона приймала у попередні моменти часу.
не залежать від того, які значення вона приймала у попередні моменти часу.
Нехай система знаходиться в одному із станів  У певні фіксовані моменти часу
У певні фіксовані моменти часу 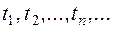 система під впливом випадкових факторів може переходити із одного стану в інший, при цьому у будь-який момент часу
система під впливом випадкових факторів може переходити із одного стану в інший, при цьому у будь-який момент часу  ймовірність для системи з’явитись у наперед заданому стані
ймовірність для системи з’явитись у наперед заданому стані 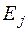 цілком визначається тим станом, у якому вони знаходились безпосередньо перед стрибком і не залежить від усіх попередніх станів, у яких система знаходилась до моменту часу
цілком визначається тим станом, у якому вони знаходились безпосередньо перед стрибком і не залежить від усіх попередніх станів, у яких система знаходилась до моменту часу  . Поведінка цієї системи описується простим ланцюгомМаркова. Отже, ланцюг Маркова є випадковим процесом з дискретним часом.
. Поведінка цієї системи описується простим ланцюгомМаркова. Отже, ланцюг Маркова є випадковим процесом з дискретним часом.
Імовірність переходу із стану  (у момент
(у момент  ) до стану
) до стану 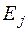 у момент
у момент  зветься перехідною ймовірністю цього ланцюга і позначається таким чином:
зветься перехідною ймовірністю цього ланцюга і позначається таким чином:
 ,
,
Ланцюг Маркова задається матрицею переходу  , елементами якої є перехідні імовірності
, елементами якої є перехідні імовірності 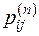 , а також ймовірності усіх станів системи у початковий момент часу
, а також ймовірності усіх станів системи у початковий момент часу 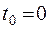 . Ці імовірності
. Ці імовірності  звуться початковими ймовірностями станів системи. Якщо всі перехідні ймовірності
звуться початковими ймовірностями станів системи. Якщо всі перехідні ймовірності 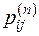 не залежать від часу (тобто
не залежать від часу (тобто  ,
,  ), тоді ланцюг Маркова називається однорідним. В цьому випадку матриця
), тоді ланцюг Маркова називається однорідним. В цьому випадку матриця  має такий вигляд:
має такий вигляд:
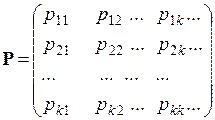
за умовою, що  та
та 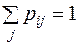 при будь-якому фіксованому
при будь-якому фіксованому 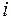 , тобто сума елементів кожного рядка дорівнює одиниці. Загальний елемент
, тобто сума елементів кожного рядка дорівнює одиниці. Загальний елемент  цієї матриці має два індекси: перший визначає номер стану
цієї матриці має два індекси: перший визначає номер стану 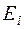 в даний момент, а другий – номер майбутнього стану
в даний момент, а другий – номер майбутнього стану 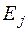 , в який перейде система. Якщо
, в який перейде система. Якщо  , то це означає, що випадкова подія, яка полягає у безпосередньому переході системи із
, то це означає, що випадкова подія, яка полягає у безпосередньому переході системи із 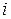 -го стану у
-го стану у 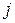 -ий неможлива. Випадок
-ий неможлива. Випадок 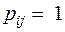 відповідає твердженню, що із
відповідає твердженню, що із 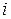 -го стану система після наступного випробування завжди переходить в
-го стану система після наступного випробування завжди переходить в 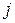 -ий стан.
-ий стан.
Позначимо ймовірність того, що система, яка керується однорідним ланцюгом Маркова, перейде із стану  в стан
в стан 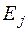 через
через  за
за  кроків. Наприклад,
кроків. Наприклад,  визначає ймовірність переходу за три кроки із другого стану в четвертий. Матриця переходів за
визначає ймовірність переходу за три кроки із другого стану в четвертий. Матриця переходів за  кроків має вигляд:
кроків має вигляд:
 .
.
Кожне значення ймовірності 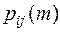 задовольняє рівнянню Маркова:
задовольняє рівнянню Маркова:
 ; (9.4)
; (9.4)
де  може приймати будь-яке ціле значення на відрізку
може приймати будь-яке ціле значення на відрізку  .
.
Безумовна ймовірність  називається абсолютною ймовірністю системі з’явитись у момент
називається абсолютною ймовірністю системі з’явитись у момент  у стані
у стані 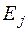 . Тоді
. Тоді  . Так, при
. Так, при  маємо:
маємо:
для 
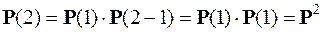 ;
;
для 

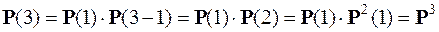 ;
;
………………………………………………………………………….
для m  .
.
Приклад. Певна сукупність робочих сімей поділена на три групи: а) ті, що не мають комп’ютер та не намагаються його купити; б) те ж ті, що не мають комп’ютер, але збираються його придбати; в) ті, що мають комп’ютер. Статистичні обстеження дали можливість оцінити ймовірності переходу сім’ї із однієї групи в іншу на протязі року. Припустимо, що матриця перехідних ймовірностей має вигляд:
 .
.
Обчислити ймовірність того, що а) сім’я, яка не має комп’ютера і не збирається його придбати, буде знаходитися в тієї ж ситуації через 2 роки; б) що сім’я, яка не має комп’ютер та має намір його придбати, буде мати комп’ютер через 2 роки.
 Розв’язання. Аналіз деяких даних цієї матриці дає можливість навести такі тлумачення:
Розв’язання. Аналіз деяких даних цієї матриці дає можливість навести такі тлумачення:
1) якщо сім’ї у попередньому році вже мали комп’ютер, то і у наступному за ним році вірогідно будуть його мати, тобто  ;
;
2) сім’ї, в яких не було комп’ютеру в попередньому році, але які збирались його придбати, матимуть змогу здійснити свій намір у наступному році з ймовірністю ;
;
3) сім’я, яка мала намір у попередньому році придбати комп’ютер, не може в наступному за цим році взагалі відмовитись від здійснення цього наміру, тобто така подія є неможливою, отже, її ймовірність дорівнює нулю ( ).
).
Аналогічно можна розглянути інші перехідні ймовірності та дати їх тлумачення.
Для обчислення шуканих ймовірностей  і
і 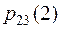 слід знайти матрицю
слід знайти матрицю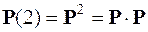 :
:
 .
.
 Таким чином, ймовірність, що сім’я, яка не має комп’ютер і не збирається його придбати, буде знаходитися в тієї ж ситуації через 2 роки дорівнює 0,49, а ймовірність того, що сім’я, що не має комп’ютер та має намір його придбати, буде мати комп’ютер через 2 роки дорівнює 0,51.
Таким чином, ймовірність, що сім’я, яка не має комп’ютер і не збирається його придбати, буде знаходитися в тієї ж ситуації через 2 роки дорівнює 0,49, а ймовірність того, що сім’я, що не має комп’ютер та має намір його придбати, буде мати комп’ютер через 2 роки дорівнює 0,51.
Ергодична теорема Маркова. Якщо існує таке натуральне число 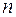 , що елементи матриці
, що елементи матриці  є строго додатними, то для кожного
є строго додатними, то для кожного  існує границя
існує границя  , яка не залежить від
, яка не залежить від  . Числа
. Числа  називаються фінальними ймовірностями станів системи:
називаються фінальними ймовірностями станів системи:
 ;
; 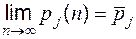 .
.
Фінальні ймовірності  є розв’язком системи лінійних рівнянь
є розв’язком системи лінійних рівнянь
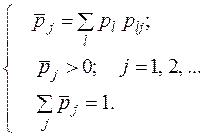 , (9.5)
, (9.5)
Ланцюг Маркова, для якого існують границі  називається ергодичним, або регулярним. Якщо ці фінальні ймовірності строго додатні, то ланцюг називається додатно - регулярним. У випадку, коли
називається ергодичним, або регулярним. Якщо ці фінальні ймовірності строго додатні, то ланцюг називається додатно - регулярним. У випадку, коли 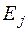 – неістотний стан, то
– неістотний стан, то  (незалежно від
(незалежно від 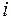 ).
).
Нехай  – одинична матриця порядку, який дорівнює порядку матриці
– одинична матриця порядку, який дорівнює порядку матриці  (розглядаються ланцюги із скінченним числом станів), а
(розглядаються ланцюги із скінченним числом станів), а 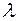 – параметр. Тоді матриця
– параметр. Тоді матриця
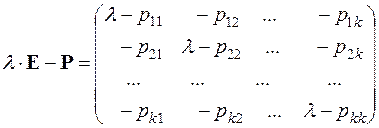
називається характеристичною матрицею даного ланцюга. Її визначник позначається через  . Усі корні рівняння
. Усі корні рівняння  є характеристичними числами матриці, одне з яких завжди дорівнює
є характеристичними числами матриці, одне з яких завжди дорівнює  , а інші по модулю не перевищують
, а інші по модулю не перевищують  .
.
Якщо ланцюг Маркова є ергодичним, то всі інші характеристичні числа по модулю строго менше одиниці та головні мінори матриці  будуть строго додатними при
будуть строго додатними при  , тобто
, тобто  .
.
Приклад. Ланцюг Маркова керується матрицею переходу:
 .
.
 Перевірити, чи є цей ланцюг ергодичним.
Перевірити, чи є цей ланцюг ергодичним.
Розв’язання. Знаходимо характеристичні числа матриці  із рівняння
із рівняння  . Підставимо дані задачі у це рівняння
. Підставимо дані задачі у це рівняння
 .
.
 Обидва розв’язки рівняння по модулю дорівнюють одиниці
Обидва розв’язки рівняння по модулю дорівнюють одиниці  . Це не задовольняє умові ергодичності, оскільки за умовою ергодичності необхідно, щоб:
. Це не задовольняє умові ергодичності, оскільки за умовою ергодичності необхідно, щоб: 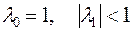 . В нашому прикладі не виконується друга умова. Отже, цей ланцюг не ергодичний.
. В нашому прикладі не виконується друга умова. Отже, цей ланцюг не ергодичний.
Фінальні ймовірності  обчислюються за формулами
обчислюються за формулами
 . (9.6)
. (9.6)
Головним мінором  є мінор, що відповідає елементу
є мінор, що відповідає елементу 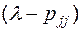 матриці
матриці 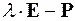 .
.
Приклад. Простий однорідний ланцюг Маркова із двома станами має матрицю переходу
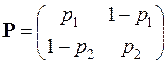 , де
, де  ,
,  .
.
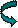 Скласти характеристичне рівняння і знайти характеристичні числа матриці та знайти фінальні ймовірності
Скласти характеристичне рівняння і знайти характеристичні числа матриці та знайти фінальні ймовірності  і
і 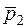 .
.
Розв’язання. Складемо характеристичне рівняння за заданою матрицею переходу. Маємо:
 .
.
Зробимо перетворення, за яким елементи першого та другого стовпчиків складаємо і записуємо замість першого, а другий стовпчик залишається без змін. Отже, маємо:

Звідси одержимо:

Отже, характеристичними числами є  і
і  .
.
Згідно з умовою задачі усі елементи матриці  є додатними:
є додатними: 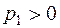 ,
,  ,
,  та
та  . Отже, ланцюг Маркова є додатно-регулярний.
. Отже, ланцюг Маркова є додатно-регулярний.
Для знаходження фінальних (граничних) ймовірностей треба знайти головні мінори визначника  :
:
 ;
; 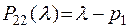 .
.
Обчислимо їх при  :
:  ,
, 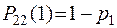 .
.
Таким чином одержуємо:
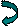
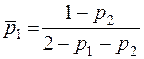 ,
,  .
.
Стан 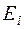 системи називається неістотним, якщо існує стан
системи називається неістотним, якщо існує стан 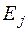 та ціле число
та ціле число  , такі, що із стану
, такі, що із стану 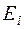 можливий перехід в стан
можливий перехід в стан 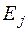 через
через  кроків, але не можливе повернення (поворот) із
кроків, але не можливе повернення (поворот) із 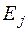 у
у 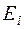 ні за яку кількість кроків:
ні за яку кількість кроків:
 ,
,  ,
,  .
.
Усі інші стани називаються істотними.
Якщо існують такі цілі числа  та
та  , що
, що  ,
,  , то стани
, то стани 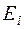 та
та 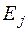 називаються зв’язаними, або сполученими. Усі істотні стани системи розбиваються на зв’язані чи ізольовані класи станів. Усі стани кожного із класів зв’язані. Потрапивши у певний клас, система в подальшому не може вийти з нього.
називаються зв’язаними, або сполученими. Усі істотні стани системи розбиваються на зв’язані чи ізольовані класи станів. Усі стани кожного із класів зв’язані. Потрапивши у певний клас, система в подальшому не може вийти з нього.
Якщо всі стани системи розбиваються на класи  , то перехідна матриця ланцюга Маркова переставленням відповідних рядків та одночасно стовпців із тими ж номерами зводиться до вигляду:
, то перехідна матриця ланцюга Маркова переставленням відповідних рядків та одночасно стовпців із тими ж номерами зводиться до вигляду:
 ,
,
де  – квадратні матриці порядків, що дорівнюють числам станів відповідного класу
– квадратні матриці порядків, що дорівнюють числам станів відповідного класу  , і більше не розкладні подібним чином. Нулі позначають підматриці, усі елементи яких дорівнюють нулю. Така матриця називається розкладною. Матриця, яку не можна привести до подібного виду, називається нерозкладною. Якщо усі
, і більше не розкладні подібним чином. Нулі позначають підматриці, усі елементи яких дорівнюють нулю. Така матриця називається розкладною. Матриця, яку не можна привести до подібного виду, називається нерозкладною. Якщо усі  при
при 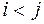 , тоді матриця називається цілком розкладною.
, тоді матриця називається цілком розкладною.
Приклад. Система може знаходитись в одному із п’яти станів і переходить із стану в стан залежно від випадку в моменти часу  Поведінка системи описується простим однорідним ланцюгом Маркова. Визначити, на які класи розділяються усі можливі стани системи, якщо матриця переходу має вигляд:
Поведінка системи описується простим однорідним ланцюгом Маркова. Визначити, на які класи розділяються усі можливі стани системи, якщо матриця переходу має вигляд:
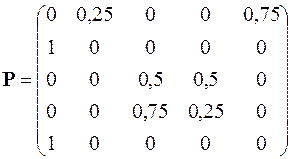 .
.
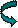 |
Розв’язання. Побудуємо імовірнісний граф (рис. 9.1).

Рис. 9.1. Граф перехідної імовірнісної матриці
Аналіз побудованого графу свідчить про розклад системи станів на два класи:  , що складається з трьох істотних станів
, що складається з трьох істотних станів 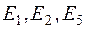 , та
, та 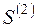 , що складається з двох станів
, що складається з двох станів  . Ці класи незалежні між собою та ізольовані. Згідно з цим аналізом робимо перетворення матриці Р, а саме, переставляємо одночасно між собою стовпці 3-й і 5-й, а також рядки 3-й та 5-й, як наслідок, отримуємо блочно-діагональну матрицю
. Ці класи незалежні між собою та ізольовані. Згідно з цим аналізом робимо перетворення матриці Р, а саме, переставляємо одночасно між собою стовпці 3-й і 5-й, а також рядки 3-й та 5-й, як наслідок, отримуємо блочно-діагональну матрицю 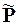 . Отже, матриця цілком розкладна.
. Отже, матриця цілком розкладна.
 .
.
 Якщо система в даний момент знаходиться в одному із станів класу
Якщо система в даний момент знаходиться в одному із станів класу  , тоді при всіх подальших змінах вона залишається в цьому класі і не переходить в інший клас, бо вони ізольовані. Те ж саме відбувається і в класі
, тоді при всіх подальших змінах вона залишається в цьому класі і не переходить в інший клас, бо вони ізольовані. Те ж саме відбувається і в класі 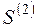 . Легко бачити, що ланцюг не є ергодичним.
. Легко бачити, що ланцюг не є ергодичним.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 9314; Нарушение авторских прав?; Мы поможем в написании вашей работы!