Определение кратного интеграла

Вопросы для обсуждения

1. Что входит в предмет и объект зоопсихологии и сравнительной психологии?

2.Какие основные теоретические и прикладные задачи решает «Зоо­психология и сравнительная психология»?

3.Какие существуют основные этапы развития научных знаний о пси­хике животных?

4. Какие основные группы методов получения эмпирических данных есть в зоопсихологии и сравнительной психологии?

5. Какие существуют основные виды эксперимента?

6. Какие методики используются в лабораторном эксперименте?

Рекомендуемая литература

Бериташвили И. С. Об образной психонервной деятельности живот­ных. — М., 1973.

Боулби Дж. Привязанность. — М., 2003.

Вагнер В.А. Сравнительная психология. — М.; Воронеж, 1998.

Выготский Л. С. Собр. соч.: В 6 т. — М., 1984.

Выготский Л. С, Лурия А. Р. Этюды по истории поведения (обезьяна, примитив, ребенок). — М.; Л., 1930.

Гальперин П. Я. Введение в психологию. — М., 1976.

Гегель Г.В. Ф. Философия природы // Соч.: В 5 т. — М.; Л., 1934. — Т. 2.

Дарвин Ч. Соч.. — М., 1953.

Дерягина М.А. Эволюционная антропология. — М., 1999.

Дьюсбери Д. Поведение животных. — М., 1981.

Ждан А. Н. История психологии: от античности до современности, ■**
М., 1997. в

Зорина З.А., Полетаева И. И. Зоопсихология: Элементарное мышление животных. — М., 2001.

Кёлер В., Коффка К. Гештальтпсихология. — М., 1998.

Ладыгина-Коте Н. Н. Дитя шимпанзе и дитя человека в их инстинк­тах, эмоциях, играх и выразительных движениях. — М., 1935.

Ладыгина-Коте Н.Н. Предпосылки человеческого мышления. — М., 1965.

Ладыгина-Коте Н.Н. Развитие психики в процессе эволюции орга­низмов. — М., 1958.

Леонтьев А. Н. Проблемы развития психики. — М., 1972.

Мак-Фарленд Д. Поведение животных: Психобиология, этология, эво­люция. - М., 1988.

Новоселова С. Л. Развитие интеллектуальной основы деятельности при­матов. — М.; Воронеж, 2001.

Рогинский Г. 3. Психика человекообразных обезьян. — Л., 1945.

Северцов А. Н. Эволюция и психика. — М., 1922.

Тайлор Э.Б. Первобытная культура. — М., 1989.

Тих И. А. Предыстория общества. — Л., 1970.

Тих Н.А. Ранний онтогенез поведения приматов. — Л., 1966.

Фабри К.Э. Основы зоопсихологии. — М., 1993.

Философская энциклопедия. — М., 1962—1970.

Фирсов Л.А. Память у антропоидов. — Л., 1972.

Фирсов Л. А. Поведение антропоидов в природных условиях. — Л., 1977.

Хайнд Р. Поведение животных. — М., 1975.

Хрустов Г. Ф. Критерий человека. — М., 1994.

Шовен Р. Поведение животных. — М., 1972.

Энгельс Ф. Диалектика природы. — М., 1969.

В этом параграфе приведены вкратце необходимые теоретические сведения, касающиеся понятия кратного интеграла.

1.1 Интеграл по параллелепипеду.

Множество 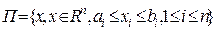будем называть стандартным относительно осей координат параллелепипедом в 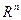(n-мерным брусом или замкнутым промежутком).

Если необходимо отметить точки а = (а₁, а₂,...,а_n) и b = (b₁, b₂,...,b_n), то будем использовать обозначение П _a,b. Таким образом, параллелепипед или замкнутый промежуток в Rⁿ есть декартово произведение отрезков, лежащих на координатных осях.

Объемом n- мерного параллелепипеда П _a,b будем называть величину произведения V(П_a,b) = 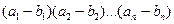. Заметим сразу, что объём открытого параллелепипеда, определяемого условиями

,

вычисляется по этой же формуле.

Пусть задан параллелепипед . Разбиения 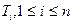, координатных отрезков , с диаметрами индуцируют разбиение параллелепипеда П _а,b на более мелкие параллелепипеды, получающиеся декартовым произведением промежутков разбиения отрезков 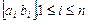. Представление параллелепипеда П _а,b в виде 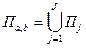называется разбиением параллелепипеда П_а,b и обозначается символом Т. Величина 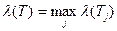называется параметром разбиения Т.

Пусть Т – разбиение параллелепипеда П и 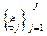– совокупность точек, таких, что . Составим интегральную сумму

. (1)

Определение 1.Если предел интегральных сумм 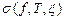при стремлении параметра разбиения к нулю существует и не зависит от выбора точек 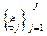и разбиения Т, то функция 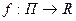интегрируема по Риману на П (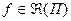), и предел

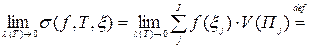
(2)

называют n-кратным интегралом от функции по параллелепипеду П.

Для введенного выше интеграла используют также следующие обозначения:

или.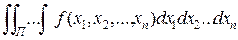

Можно определить интеграл по параллелепипеду и с помощью сумм Дарбу. Пусть функция 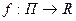ограничена на П и T – разбиение П. Положим

, , ,

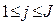Составим суммы

,,

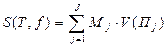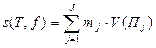и пусть

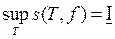, , (3)

где верхняя и нижняя грани берутся по всевозможным разбиениям Т.

Заметим, что если функция ограничена на замкнутом параллелепипеде П, то, интегрируема она или нет, верхняя грань всех нижних сумм и нижняя грань всех верхних сумм всегда существуют.

Суммы 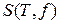и соответственно называют верхней и нижней суммами Дарбу, а величины и соответственно верхним и нижним интегралами Дарбу функции f, соответствующими разбиению Т. Для любой ограниченной функции 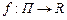имеем .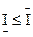

В том случае, когда функция непрерывна, верхняя и нижняя суммы Дарбу являются частным случаем интегральных сумм в формуле(2).

Определение 2.Если , то функция называется интегрируемой по Риману на П, число I называется интегралом Римана от f по параллелепипеду П и обозначается

I= .

Множество интегрируемых по Риману на П функций будем обозначать (П).

Чтобы подчеркнуть, что в данных выше двух определениях 1 и 2 речь идет об интеграле от функции многих переменных (заданной на параллелепипеде 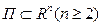), введённый интеграл называют n- кратным (двойным, тройным и т. д.) в соответствии с размерностью Rⁿ.

Определение 3. Множество имеет n-мерную меру нуль (или есть множество меры нуль в смысле Лебега), если для любого существует покрытие множества М не более чем счетной системой 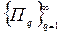n -мерных замкнутых параллелепипедов (промежутков), сумма объемов которых не превышает : .

В этом определении вместо замкнутых параллелепипедов можно брать открытые.

Напомним некоторые свойства множеств меры нуль:

1) если множество М имеет меру нуль и , то A имеет меру нуль;

2) объединение конечного или счётного числа множеств меры нуль есть множество меры нуль;

3) множество, содержащее конечное или счётное число точек, имеет меру нуль;

4) если – замкнутое ограниченное множество и функция 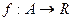непрерывна на A, то график функции 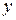на A, т.е. множество

есть множество меры нуль в .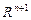

Заметим, что никакое открытое множество не является множеством меры нуль. Так, интервал 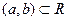является открытым множеством в пространстве R и, значит. не является в R множеством меры нуль. Если же рассматривать этот интервал (а, b) на оси ОХ в двумерном пространстве R², то он будет в R² множеством меры нуль и не будет открытым множеством в R².

Параллелепипед П _a,b не является множеством меры нуль в .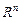

Будем говорить, что некоторое свойство имеет место почти всюду на М, если это свойство нарушается лишь на таком подмножестве М, которое имеет меру нуль.

Теорема 1.(Критерий Лебега). Для интегрируемости функции 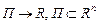по замкнутому параллелепипеду П, необходимо и достаточно, чтобы была ограничена на П, и непрерывна почти всюду на П.

Вычисление кратных интегралов осуществляется с помощью теоремы Фубини.

Теорема 2(Теорема Фубини). Пусть - параллелепипед в , являющийся прямым произведением параллелепипедови . Если функция интегрируема на , то интегралы

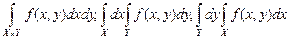
существуют одновременно и равны между собой [2],т.е.

(4)

Символ следует понимать так: при фиксированном значении вычисляется интеграл 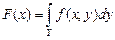по параллелепипеду Y, затем полученная функция интегрируется по параллелепипеду X.

При этом, если для некоторого интеграл не существует, то F(x) полагается равным любому числу из промежутка [], где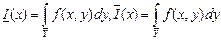. Из доказательства теоремы следует тот факт, что множество значений , для которых 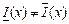есть множество меры нуль. Аналогичный смысл имеет символ .

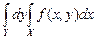В отличие от интеграла по -мерному параллелепипеду , который называют кратным интегралом, последовательно вычисляемые интегралы от 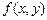по Y, затем по X, или по X, затем по Y, называют повторными интегралами от этой функции.

2.1. Вычисление двойных интегралов по определению. Способ вычисления кратных интегралов в соответствии с данными выше определениями 1 и 2 §1не является, вообще говоря, удобным для практического применения. Тем не менее, понимание алгоритма введения кратного интеграла важно для усвоения этого понятия. В случае 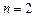параллелепипедами в 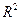будут прямоугольники, а двумерным объёмом- площадь. Пусть задана функция , D ,.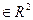

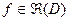В частности, D может представлять собой ограниченную область в плоскости XOY, замыканием которой является замкнутая кусочно-гладкая кривая без точек самопересечения.

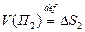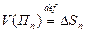Пусть разбиение - это разбиение D произвольным образом на n прямоугольников ,имеющих площади , , …, и диаметры 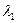, , 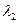…, соответственно (диаметром назовем наибольшую диагональ замыкания прямоугольника разбиения). Параметр разбиения 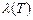=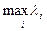- наибольший из диаметров , 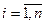. Фиксируя в каждом прямоугольнике произвольную точку 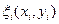, составим интегральную сумму (1). Она будет иметь вид:

Предел этой интегральной суммы при стремлении параметра разбиения к 0, будет двойным интегралом от функции 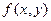по множеству :

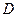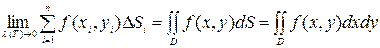. (8)

Существование предела (8) и независимость его от способа разбиения и выбора точек 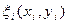, , 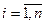следует из интегрируемости функции 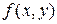на жордановом множестве .

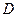Геометрический и механический смысл двойного интеграла. Если , то интеграл (5) равен площади 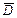, т.е.

.

Если на множестве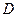, то двойной интеграл (8) равен объему цилиндрического тела, ограниченного сверху поверхностью 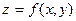, сбоку – цилиндрической поверхностью с образующими, параллельными оси OZ и снизу - областью 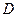плоскости XOY (геометрический смысл).

Если рассматривать функцию как функцию плотностинекоторой плоской пластины D, то интеграл (8) равен массе этой плоской пластины (механический смысл): .

Дата добавления: 2014-01-15