Определение евклидова пространства

Определение. Вещественное линейное пространство называется евклидовым, если на нем выделена симметричная положительно определенная билинейная форма.

Другими словами, на пространстве выделена билинейная форма 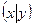, обладающая свойствами:

1). =;

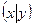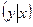2). =+;

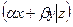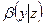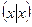
3). для всех .

Примеры. 1). Скалярное произведение в обычном трехмерном пространстве геометрических векторов превращает его в евклидово пространство.

В общем случае эту выделенную форму на произвольном пространстве тоже будем называть скалярным произведением.

2). Пусть - арифметическое векторное пространство строк длины 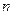. Введем на скалярное произведение следующим образом. Если 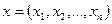, , 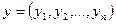то . Легко проверить, что эта форма билинейная, симметричная и положительно определенная.

3). Пусть - линейное пространство функций, непрерывных на отрезке 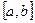. Можно задать скалярное произведение в этом пространстве таким образом:

.

16.2. Длина вектора в евклидовом пространстве. Пусть - евклидово пространство со скалярным произведением .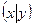

Определение. Длиной (нормой) вектора 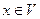будем называть неотрицательное действительное число

.

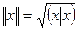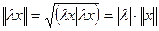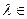Заметим, что если , то . Далее, , R.

Вектор длины 1 называют нормированным. Любой вектор можно нормировать, умножив его на подходящее число, а именно для вектора имеем:

.

Дата добавления: 2014-01-15