
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоремы дифференциального исчисления. Правило Лопиталя
|
|
|
|
Функция 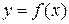 , определенная во всех точках промежутка
, определенная во всех точках промежутка  , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т.е.
, называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т.е.
если 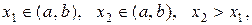 то при
то при
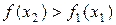 – возрастающая,
– возрастающая, 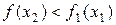 – убывающая.
– убывающая.
Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: 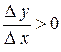 . Для убывающей функции эти приращения имеют разные знаки, в силу чего
. Для убывающей функции эти приращения имеют разные знаки, в силу чего 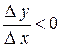 . Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
. Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
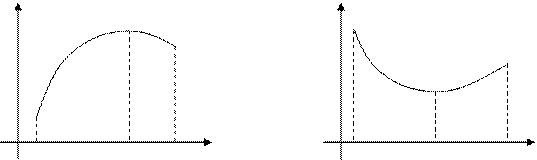
Точка 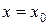 называется точкой максимума (минимума) непрерывной функции
называется точкой максимума (минимума) непрерывной функции 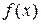 , а значение
, а значение 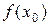 называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки
называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки 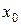 такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке
такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке 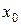 , т.е. меньше (больше), чем максимум (минимум)
, т.е. меньше (больше), чем максимум (минимум) 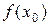 (рисунок 1).
(рисунок 1).
 у max у
у max у
min
f (х 0) f (х 0)
О х0–d х0 х0+d х О х0–d х0 х0+d х
| точка максимума | точка минимума |
Рисунок 1
Из определений точек экстремума следует, что вне d-окрестности точки экстремума поведение функции произвольно, т.е. понятия максимума и минимума функции носят характер локальных (местных), а не абсолютных понятий.
Чтобы установить признаки возрастания и убывания и признаки экстремума функций рассмотрим ряд важных теорем математического анализа, на которые опираются все дальнейшие исследования функций.
Теорема Ферма. Если функция 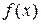 непрерывна в промежутке
непрерывна в промежутке  , в некоторой внутренней точке х 0 этого промежутка достигает максимума (или минимума) и дифференцируема в этой точке, то ее производная в этой точке равна нулю:
, в некоторой внутренней точке х 0 этого промежутка достигает максимума (или минимума) и дифференцируема в этой точке, то ее производная в этой точке равна нулю: 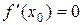 .
.
Предположим для определенности, что х 0 – точка максимума. Тогда для любой точки 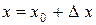 из интервала
из интервала  выполняется неравенство
выполняется неравенство 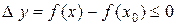 . Поэтому
. Поэтому 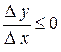 , если
, если 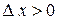 и
и 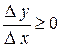 , если
, если 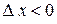 . Переходя к пределам, получим
. Переходя к пределам, получим
 и
и 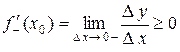 .
.
Оба неравенства будут выполняться, если 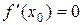 .
.
Геометрический смысл теоремы Ферма состоит в том, что касательная к графику функции 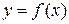 в точке
в точке 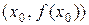 параллельна оси Ох, если х 0 – точка максимума или минимума функции
параллельна оси Ох, если х 0 – точка максимума или минимума функции 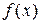 на интервале
на интервале  (рисунок 2).
(рисунок 2).
В точке максимума (минимума) х 0 производная 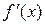 может не существовать (рисунок 3)
может не существовать (рисунок 3)
 у max у
min
f (х 0) f (х 0)
О a х0 b х О a х0 b х
Рисунок 2 у max у
min
f (х 0) f (х 0)
О a х0 b х О a х0 b х
Рисунок 2
| у max min О a х 0 b х Рисунок 3 |
Теорема Ролля. Пусть функция 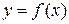 :
:
1) непрерывна на отрезке 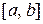 ;
;
2) дифференцируема на интервале  ;
;
3) на концах отрезка принимает равные значения 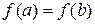 .
.
Тогда существует точка 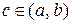 , в которой
, в которой 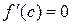 . Так как функция непрерывна на отрезке
. Так как функция непрерывна на отрезке 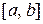 , то она принимает в некоторых точках
, то она принимает в некоторых точках 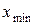 и
и 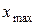 минимальное и максимальное значения:
минимальное и максимальное значения: 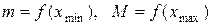 . Если
. Если 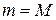 , то
, то 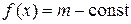 и в любой точке интервала
и в любой точке интервала  производная
производная 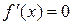 . Поэтому можем считать, что
. Поэтому можем считать, что 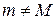 . Положим
. Положим 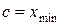 , если
, если 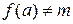 , и
, и 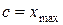 , если
, если 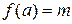 . При таком определении с имеем
. При таком определении с имеем 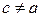 . Поскольку
. Поскольку 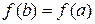 , то
, то 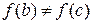 , поэтому
, поэтому 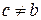 . Итак, с – это точка максимума или минимума функции
. Итак, с – это точка максимума или минимума функции 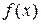 и
и 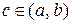 . По теореме Ферма
. По теореме Ферма 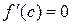 .
.
Геометрический смысл теоремы Ролля: на графике функции 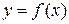 найдется по крайней мере одна точка, в которой касательная к графику параллельна оси Ох.
найдется по крайней мере одна точка, в которой касательная к графику параллельна оси Ох.
В частном случае, когда 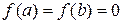 , теореме Ролля можно дать новое толкование: между двумя нулями дифференцируемой функции всегда заключен по крайней мере один нуль ее производной.
, теореме Ролля можно дать новое толкование: между двумя нулями дифференцируемой функции всегда заключен по крайней мере один нуль ее производной.
Теорема Лагранжа. Пусть функция 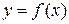 непрерывна на отрезке
непрерывна на отрезке 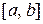 и дифференцируема на интервале
и дифференцируема на интервале  . Тогда существует такая точка
. Тогда существует такая точка 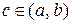 , что
, что
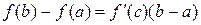 . (2)
. (2)
Формула (2) называется формулой конечных приращений.
Введем вспомогательную функцию
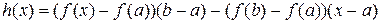 .
.
Тогда
1) 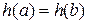 ;
;
2) 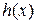 непрерывна в тех же точках, в которых непрерывна функция
непрерывна в тех же точках, в которых непрерывна функция 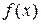 , т.е.
, т.е. 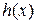 непрерывна на
непрерывна на 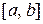 и дифференцируема в
и дифференцируема в  . По теореме Ролля существует точка
. По теореме Ролля существует точка 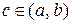 , в которой
, в которой 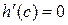 . Так как
. Так как 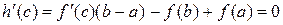 , то в точке с выполняется равенство (2).
, то в точке с выполняется равенство (2).
Теорема Коши. Пусть функции 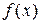 и
и 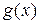 непрерывны на отрезке
непрерывны на отрезке 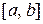 и дифференцируемы на интервале
и дифференцируемы на интервале  . Пусть, кроме того,
. Пусть, кроме того, 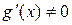 на
на  . Тогда существует точка
. Тогда существует точка 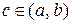 , такая, что
, такая, что
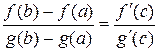 .
.
Теорема Лагранжа является частным случаем теоремы Коши, когда 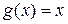 .
.
Раскрытие неопределенностей по правилу Лопиталя. Раскрытием неопределенностей в математическом анализе называется отыскание предела 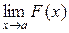 , когда функция
, когда функция 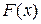 непрерывна вблизи точки
непрерывна вблизи точки 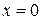 , но не определена в самой этой точке, а непосредственная подстановка в формулу этой функции значения
, но не определена в самой этой точке, а непосредственная подстановка в формулу этой функции значения 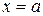 приводит к выражению неопределенного вида:
приводит к выражению неопределенного вида:
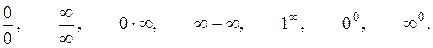
Основными видами неопределенностей являются следующие два: 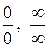 .
.
Для этих двух видов неопределенностей справедлива теорема Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных
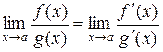 .
.
Правило Лопиталя позволяет во многих случаях найти предел 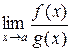 вида
вида 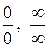 или, как говорят, раскрыть неопределенность.
или, как говорят, раскрыть неопределенность.
Замечание 1. Другие виды неопределенностей можно свести к основным видам.
Замечание 2. Правило Лопиталя можно применять повторно.
Пример Найти 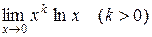 . Это неопределенность вида
. Это неопределенность вида 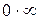 . Представим данный предел в виде
. Представим данный предел в виде 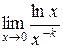 ; это уже будет неопределенность вида
; это уже будет неопределенность вида 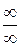 , к которой применимо правило Лопиталя.
, к которой применимо правило Лопиталя.
Поэтому 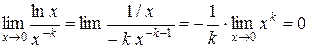 .
.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 686; Нарушение авторских прав?; Мы поможем в написании вашей работы!