
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изоморфизм векторных пространств одинаковой размерности.
|
|
|
|
Дополнение линейно независимой системы векторов векторного пространства V до базиса. Подпространство векторного пространства. Критерий подпространства. Пересечение и сумма подпространств.
Лемма 1. Любая линейно независимая система векторов векторного пространства Vn может быть дополнена до базиса пространства Vn.
Доказательство. Пусть 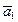 ,
, 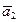 , …,
, …,  (1) — линейно независимая система векторов n-мерного векторного пространства Vn. Пусть (2)
(1) — линейно независимая система векторов n-мерного векторного пространства Vn. Пусть (2) 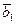 ,
, 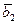 ,…,
,…,  — базис пространства Vn. Рассмотрим систему векторов
— базис пространства Vn. Рассмотрим систему векторов 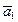 ,
, 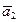 , …,
, …,  ,
, 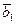 ,
, 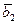 ,…,
,…,  (3). Система векторов (3) конечная и она содержит максимальную линейно независимую подсистему (2). Следовательно, система векторов (2) является базисом системы векторов (3). Так как любые два базиса системы векторов (3) состоят из одного и того же числа векторов n, то в конечной системе векторов (3) можно построить максимальную линейно независимую подсистему, содержащую систему векторов (1). Тогда она будет состоять из n векторов и, значит, будет являться базисом пространства V.
(3). Система векторов (3) конечная и она содержит максимальную линейно независимую подсистему (2). Следовательно, система векторов (2) является базисом системы векторов (3). Так как любые два базиса системы векторов (3) состоят из одного и того же числа векторов n, то в конечной системе векторов (3) можно построить максимальную линейно независимую подсистему, содержащую систему векторов (1). Тогда она будет состоять из n векторов и, значит, будет являться базисом пространства V.
Определение 4. Пусть Н – непустое подмножество векторного пространства V над полем Р. Н называется подпространством пространства V, если Н само является векторным пространством над полем Р.
Теорема (критерий подпространства). Пусть Н – непустое подмножество пространства V над полем Р. Н является подпространством V тогда и только тогда, когда выполняются следующие условия:
1) Для любых  ,
,  из Н
из Н  +
+  Î Н;
Î Н;
2) для любого a из Р и любого  из Н выполняется a
из Н выполняется a Î Н.
Î Н.
Доказательство. Необходимость. Пусть Н – подпространство пространства V. Тогда по определению Н является векторным пространством над полем Р и H замкнуто относительно сложения векторов и умножения вектора на скаляр из поля Р. Следовательно, условия 1) и 2) выполняются.
Достаточность. Пусть выполняются условия 1) и 2) теоремы. Т.к. (-1)ÎР, то по условию 2) для любого  из Н (-1)
из Н (-1) = -
= -  Î Н. Тогда, по критерию подгруппы, Н является подгруппой аддитивной абелевой группы V, и, следовательно, Н само является аддитивной абелевой группой. Т.к. обобщенные дистрибутивные и ассоциативные законы выполняются в V, то они выполняются и в Н. Кроме того, 1
Î Н. Тогда, по критерию подгруппы, Н является подгруппой аддитивной абелевой группы V, и, следовательно, Н само является аддитивной абелевой группой. Т.к. обобщенные дистрибутивные и ассоциативные законы выполняются в V, то они выполняются и в Н. Кроме того, 1 =
= для любого
для любого  из Н. Следовательно, Н удовлетворяет определению векторного пространства над полем Р и, значит, по определению Н является подпространством пространства V.
из Н. Следовательно, Н удовлетворяет определению векторного пространства над полем Р и, значит, по определению Н является подпространством пространства V.
Определение 2. Пусть V1, V2,…, Vs — подпространства векторного пространства V над полем Р. Множество М={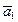 +
+ 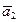 + …+
+ …+ 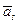 ½
½  Î Vi, i=
Î Vi, i= } называется суммой подпространств V1, V2,…, Vs и обозначается М = V1 + V2 +…+ Vs.
} называется суммой подпространств V1, V2,…, Vs и обозначается М = V1 + V2 +…+ Vs.
Лемма 2. Пусть V1, V2,…, Vs — подпространства векторного пространства V над полем Р. Тогда
1) Н = V1 + V2 +…+ Vs является подпространством пространства V;
2) D = V1 Ç V2 Ç…Ç Vs является подпространством пространства V.
Доказательство. 1) Пусть  ,
, 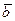 Î Н. Тогда по определению суммы подпространств
Î Н. Тогда по определению суммы подпространств
 =
=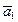 +
+ 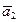 + …+
+ …+ 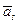 ,
, 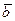 =
= +
+ 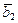 + …+
+ …+  , где
, где  ,
,  Î Vi, i=
Î Vi, i= . Найдём сумму
. Найдём сумму
 +
+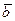 = (
= (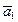 +
+  ) + (
) + (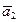 +
+ 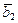 ) +…+ (
) +…+ (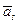 +
+  ). Так как
). Так как 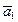 +
+  Î V1,
Î V1, 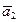 +
+ 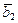 ÎV2, …,
ÎV2, …, 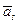 +
+  ÎVs, то по определению
ÎVs, то по определению  +
+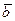 Î Н. Значит, Н замкнуто относительно сложения векторов. Далее, для любого a из Р и любого
Î Н. Значит, Н замкнуто относительно сложения векторов. Далее, для любого a из Р и любого  из Н выполняется:
из Н выполняется:
a  = a(
= a(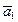 +
+ 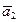 + …+
+ …+ 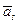 )= a
)= a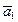 + a
+ a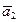 + …+ a
+ …+ a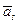 .
.
Поскольку a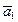 Î V1, a
Î V1, a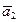 Î V2, …, a
Î V2, …, a 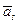 Î Vs, то по определению a
Î Vs, то по определению a Î Н и Н замкнуто относительно умножения на скаляры из поля Р. По критерию подпространства, Н является подпространством пространства V.
Î Н и Н замкнуто относительно умножения на скаляры из поля Р. По критерию подпространства, Н является подпространством пространства V.
2) Доказательство проводится аналогично.
Определение. Пусть V1 и V2 — векторные пространства над одним и тем же полем P. Говорят, что V1 изоморфно V2 (обозначается V1 @ V2), если существует взаимно-однозначное отображение j пространства V1 на V2 такое, что выполняются следующие условия:
1) j( +
+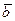 ) = j(
) = j( ) + j(
) + j(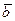 ) для любых
) для любых  и
и 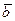 из V1;
из V1;
2) j(a  ) = aj(
) = aj( ) и для любых
) и для любых  Î V1 и aÎР.
Î V1 и aÎР.
Теорема. Пусть V — векторное пространство над полем P и dimPV=n. Тогда V@Pn, гдеPn — арифметическое n-мерное векторное пространство.
Доказательство. Пусть 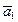 ,
, 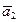 , …,
, …, 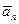 — базис векторного пространства V над полем P. Тогда для любых
— базис векторного пространства V над полем P. Тогда для любых  и
и 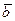 из V существует единственное разложение по базису:
из V существует единственное разложение по базису:
 =a1
=a1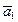 + a2
+ a2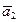 + … + a n
+ … + a n 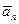 =
=  и
и 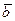 = b1
= b1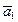 + b2
+ b2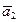 + … + b n
+ … + b n 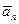 =
= 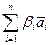 .
.
Зададим соответствие j по правилу j( ) = (a1, a2, …, an)для любого
) = (a1, a2, …, an)для любого  =
= Î V, т.е. каждому вектору из V поставим в соответствие кортеж его координат. В силу единственности разложения вектора по базису, j является отображением V в Pn. Покажем, что j — биекция. Действительно, для любого (g1, g2, …, gn) Î Pn, существует
Î V, т.е. каждому вектору из V поставим в соответствие кортеж его координат. В силу единственности разложения вектора по базису, j является отображением V в Pn. Покажем, что j — биекция. Действительно, для любого (g1, g2, …, gn) Î Pn, существует 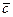 =g1
=g1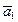 + g2
+ g2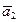 + … + g n
+ … + g n 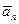 Î V, такой что j(
Î V, такой что j(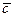 )= (g1, g2, …, gn). Следовательно, j — сюръекция.
)= (g1, g2, …, gn). Следовательно, j — сюръекция.
Проверим инъективность j. Пусть j( )=j(
)=j(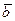 ). Тогда по определению j, имеем
). Тогда по определению j, имеем
(a1, a2, …, an) = (b1, b2, …, bn). Это равенство возможно только в случае ai=bi, для всех i=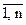 . Но тогда
. Но тогда  =
=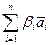 , что означает
, что означает  =
=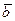 . Следовательно, j — инъективно. Таким образом, отображение j биективно.
. Следовательно, j — инъективно. Таким образом, отображение j биективно.
Проверим выполнимость условий 1) и 2) определения изоморфизма векторных пространств.
j( +
+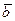 ) = j(
) = j( +
+ 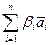 ) = (коммутативность «+» на V, обобщенный дистрибутивный закон)= j(
) = (коммутативность «+» на V, обобщенный дистрибутивный закон)= j( ) = (a1+b1, a2+b2, …, an+bn) = (a1, a2, …, ar) + (b1, b2, …, bn) =j(
) = (a1+b1, a2+b2, …, an+bn) = (a1, a2, …, ar) + (b1, b2, …, bn) =j( +
+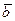 ) для любых
) для любых  и
и 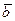 из V, т.е. условие 1) выполняется.
из V, т.е. условие 1) выполняется.
Для любого aиз Р и любого  Î Vj(a
Î Vj(a ) = j(a
) = j(a ) = (обобщенный дистрибутивный закон, обобщенная ассоциативность) = j(
) = (обобщенный дистрибутивный закон, обобщенная ассоциативность) = j(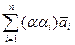 ) =(aa1, aa2, …, aan)= a(a1, a2, …, an) = aj(
) =(aa1, aa2, …, aan)= a(a1, a2, …, an) = aj( ), т.е. выполняется условие 2) определения. Значит, j является изоморфизмом векторного пространства V на арифметическое n-мерное векторное пространство Pn, т.е.V@Pn. Теорема доказана.
), т.е. выполняется условие 2) определения. Значит, j является изоморфизмом векторного пространства V на арифметическое n-мерное векторное пространство Pn, т.е.V@Pn. Теорема доказана.
Следствие. Любые два n-мерных векторных пространства над полем P изоморфны.
Доказательство. Пусть V1 и V2 — n-мерные векторные пространства над полем P. Тогда по теореме V1@Pn и V2@Pn. Т.к. отношение изоморфизма векторных пространств является отношением эквивалентности, то оно симметрично и транзитивно. Из V2@Pn следует Pn @ V2. Из V1@Pn и Pn @ V2 получаем V1@V2. Следствие доказано.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 842; Нарушение авторских прав?; Мы поможем в написании вашей работы!