Уравнение малых поперечных колебаний струны

Уравнение гиперболического типа.

Постановка краевых задач

Основные уравнения математической физики.

Уравнения с частными производными второго порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессом колебаний (струн, стержней, мембран ит.д.). Ограничимся рассмотрением класса линейных уравнений.

Рассмотрим натянутую струну, закреплённую на концах. Под струной будем понимать упругую тонкую нить, которая может свободно изгибаться, то есть не оказывать ни какого сопротивления формы, но не изменять длины. Сила натяжения действующая на струну предполагается значительной, так чтобы можно пренебречь силой тяжести (для струны). Пусть струна, длина которой 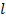, в положении равновесия направлена по оси х. Рассматривать будем только малые поперечные колебания струны, полагая, что все движение будет происходить в одной плоскости, и все точки струны будут двигаться по оси х.

Функция u(x)описывает отклонение от положения в момент времени t. Будем рассматривать малые колебания. С точки зрения математики это означает что:

(1)

Пользуясь этим условием, определим удлинение, испытываемое участком струны 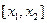. Длина дуги этого участка равна

(2)

В пределах нашей точности (1), уравнения участков струны в процессе колебаний не происходит. Таки образом, в силу закона Гука следует, что величина натяжения T в каждой точке не меняется со временем. С другой стороны можно показать, что натяжении не зависит и от координаты x, т.е.

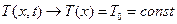
Согласно принципу Даламбера сумма действующих в проекции сил равна нулю.

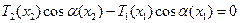(3)

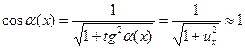(4)

Где – это угол касательной к струне.

В силу произвольност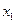и и 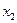, можно утверждать, что напряжение не зависит от х: .

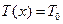Для вывода уравнения поперечных колебаний струны воспользуемся вторым законом Ньютона. Импульс участка струны 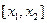вдоль оси u равен

(5)

Где–линейная плотность струны. Согласно второму закону Ньютона, приравняем изменение импульса элемента струны за время импульсу всех сил, действующих на участок струны 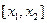вдоль оси u равен. Таким образом, получаем интегральное уравнение

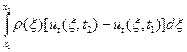(6)

Найдем импульс всех сил действующие на участки струны. Проекция сил натяжения действует на вертикальную ось:

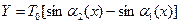
Сумма проекции сил на вертикальную ось:

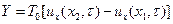
Где- время

Проекция сил натяжения:

(7)

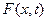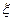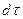Импульс внешних сил, будем считать что эта сила непрерывна распределяется по струне с плотностью. Интегрируем по и , получаем:

(8)

Импульс сил сопротивления:

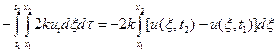(9)

k – коэффициент сопротивления.

Выражение (6) приравниваем к выражению (8)+(7)+(9) и получаем:

(10)

интегральное уравнение для малых поперечных волн. Перейдем к дифференциальной форме, для этого должны существовать две непрерывные функции. Применяя теорему о среднем и теорему Лагранжа, из формулы (10) получим:

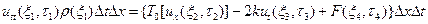(11)

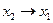
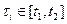
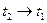
Делим на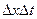

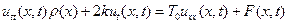(12)

Получили уравнение малых поперечных волн в дифференциальной форме или его еще называют волновое уравнение.

Для однородной среды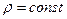тогда уравнение (12)становится проще:

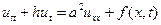(13)

Получили уравнение вынужденных малых колебаний.

Где; ; .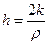

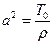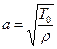Если пренебречь силой сопротивления, то получим уравнение вынужденных колебаний без учёта сопротивления:

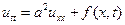(14)

Без отсутствия внешних сил уравнение (14) примет вид:

(15)

Или

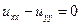
Это простейшее уравнение гиперболического типа. Оно описывает свободные колебания струны.

Дата добавления: 2014-01-15