Тема: Моделі систем

1. Формальні і змістовні моделі

Побудову моделі системи ми розглядаємо як етап вирішення проблемної ситуації, етап вивчення системи. Існує багато моделей систем, які суттєво відрізняються одна від одної. Розглянемо їх.

Формальні моделі - це окремі типи моделей, подані у формальному, описовому вигляді, в який входять головні ознаки, за якими дана модель, суттєво відрізняється від інших. В описі формальної моделі даються також правила її побудови, складові частини моделі, зв’язки між частинами, вигляд моделі в цілому.

Формальна модель має загальний характер без конкретного на­повнення є немовби каркасом, на основі якого можна побудувати ці­лий ряд змістовних моделей. Формальних моделей існує обмежена кількість. В описі формальної моделі абстрагуються від змісту, внут­рішнього наповнення, предметної області, для якої створюється мо­дель. Формальні моделі є абстрактними моделями, описаними абстра­ктною, найбільш загальною мовою. Залежно від рівня абстракції фор­мальні моделі можуть охоплювати різну кількість систем. До форма­льних моделей самого високого рівня абстракції відносяться моделі „Чорний ящик”, “Склад системи”, “Структура системи”, “Структурна схема”.

Змістовні моделі - це моделі, наповнені поняттями даної предметної області. Вони будуються на основі формальних моделей, що служать шаблоном, зразком для побудови змістовних моделей.

Створення змістовної моделі - це процес інтерпретації формаль­ної моделі на мові певної предметної області. Інтерпретація - це вста­новлення відповідності між формальною і змістовною моделями сис­теми. Інтерпретація (від лат. “interpretatio” - пояснення, тлумачення) визначається як сукупність значень (змісту), які певним чином нада­ються елементам деякої системи, теорії чи моделі. У математиці інтер­претація - це встановлення відповідності, пояснення положень деякої формальної теорії на мові певної змістовної системи, причому поло­ження змістовної системи повинні бути визначені незалежно від фор­мальної системи. Інтерпретація вважається повною, якщо кожному елементу формальної системи відповідає певний елемент змістовної системи.

У системному аналізі змістовні моделі систем будують на основі формальних моделей. Формальна модель задає основні положення цієї моделі, її елементи, зв’язки, правила побудови, а змістовна модель наповнює ці елементи і зв’язки певним змістом, узятим з конкретної системи, яка досліджується. Таким чином встановлюється відповідність між елементами формальної моделі та елементами змістовної моделі системи. У випадках, коли встановлено, що елементи формальної моделі однозначно відповідають елементам змістовної системи, існує взаємно однозначна відповідність, то всі результати, отримані для формальної моделі, підтверджуються в змістовній моделі.

Формальних моделей ми знаємо обмежену кількість, а змістовних моделей може бути побудовано в необмеженій кількості. Це викликано тим, що за однією формальною моделлю можна побудувати змістовні моделі для безлічі систем навколишнього світу. З іншого боку, навіть для однієї системи за однією і тією ж формальною моделлю можна побудувати необмежену кількість змістовних моделей, залежно від цілей моделювання, точки зору та рівня знань того, хто будує модель. Якою буде побудована змістовна модель залежить від цілей моделювання, складності системи, досвіду і знань аналітика та інших факторів. Успіхи вивчення систем і вирішення проблем системного аналізу значною мірою залежить від того, в якій мірі аналітик володіє набором формальних моделей і вміє їх інтерпретувати.

2. Модель типу „ Чорний ящик ”

Найпростіша формальна модель ящик”. Вигляд її показано на рис. 11.

Рис. 11 - Модель типу “Чорний ящик”

Формальна модель типу “Чорний ящик” являє собою прямокутник, що означає систему. Він обмежений границями, стрілками зображено входи (вхідні величини) та виходи (вихідні величини) системи. Входи – це те, що система використовує для своєї діяльності, з чим вона працює і що перетворює. Виходи – результат діяльності системи, те, що вона створює, в що перетворює вхідні величини відповідно до своїх функцій.

На перший погляд дана модель досить проста і не заслуговує великої уваги. Але ця простота дуже обманлива, за нею скрито багато складних речей. Ці речі виявляються, як тільки від формальної моделі ми переходимо до побудови змістовної моделі.

Модель „Чорний ящик” при своїй простоті є досить корисною. По-перше, навіть така проста модель може багато сказати про систему. Маючи справу з невідомими для нас об’єктами, якщо ми знаємо їх вхідні й вихідні величини, ми вже досить багато знаємо про ці об’єкти. Розглянемо приклади біології, медицини. Вивчаючи клітину, ми з’ясовуємо, що в неї надходить і що є на виході. Такі знання вже багато говорять про функції клітини і роль її в організмі. Наші знання про органи людини: серце, легені, нирки та ін. описуються моделлю “чорний ящик”. Такі знання про ядро клітини, мітохондрії та інші форми клітини достатні для лікування багатьох захворювань. Для повсякденного життя знання багатьох систем на рівні “чорного ящика” буває достатнім і потреби в подальшому вивченні не виникає. Наприклад, візьмемо телевізор. Нам достатньо знати його входи, як і що потрібно подати, змінити, яку кнопку натиснути і який регулятор повернути і ми можемо вільно ним користуватися. Потреби подальшого вивчення його в більшості людей немає. Аналогічна ситуація з холодильником, пральною машиною та багатьма іншими приладами.

По-друге, деколи подання системи у вигляді “чорного ящика” є єдиним способом вивчення системи. Наприклад, вивчення психології людини. Психологи вивчають способи дії на свідомість людини і результати цієї дії. Криміналісти також використовують модель “Чорний ящик”. Дослідження на так званому „детекторі правди” виконуються на рівні моделі “Чорний ящик”: вхід – це слова, вихід - зміни ритму дихання, тику крові, електричних імпульсів мозку, зміна провідності шкіри, виділення поту і т. ін.

З математичної точки зору модель типу „Чорний ящик” подають у вигляді певного оператора R, який перетворює вхідні величини на вихідні. Цей оператор може бути простим або досить складним. Вивченням систем на такому рівні займається цілий ряд наукових дисциплін, які досягають значних практичних результатів.

Розглянемо питання побудови змістовної моделі системи типу “Чорний ящик”. Як було відзначено, побудова змістовної моделі - це інтерпретація формальної моделі на певну предметну область. Тобто для побудови змістовної моделі треба присвоїти елементам формальної моделі певні значення. Якщо, наприклад, потрібно побудувати змістовну модель системи “телевізор”, то ми як вхідні величини можемо розглядати електричний струм живлення телевізора і електромагнітні хвилі, що надходять на антену, а як вихідні величини – зображення, звук, їх характеристики. Щоправда, необхідно ще врахувати органи керування телевізора і наші дії при регулюванні його роботи. Отже, на перший погляд побудова змістовної моделі будь-якої системи по формальній моделі “Чорний ящик” досить проста. Проте за цією простотою можуть приховуватися досить складні речі.

Перше запитання, що виникає при побудові змістовної моделі, визначення границь системи. Встановити їх не завжди просто, це залежить як від самої системи, так і від цілей моделювання, від точки зору моделювання та інших факторів. Наприклад, система “річка”. Тут ми вперше зустрічаємось з проблемою визначення границь системи. Де пролягає границя системи, де ми її визначимо, як це розглянуто в попередніх розділах, залежить від цілого ряду факторів.

Розглянемо ще кілька прикладів. Майже чітко означена система “Людина”. Але і тут виникають складності при визначенні границь. Одяг входить до даної системи чи ні? Людина без одягу? Вважаємо, що входить. Але одяг може висіти в шафі. Коли він стає системою “Людина”? А дощова накидка стає системою "людина"? А парасолька? Котлета, яку ми з’їдаємо за обідом, в який момент вона входить в систему „Людина”. Повітря, яке ми видихаємо, наше біополе, де воно закінчується? Вирішення цих питань значною мірою залежить від цілей моделювання, точки зору.

Система „Залізничний вокзал”, де її границі? Привокзальна площа для транспорту входить до неї чи ні? А залізничні колії, на якій відстані віднести їх до системи “вокзал”?

Студент на канікулах входить до системи “ВУЗ” чи ні?

Отже, вже перше питання визначення границь системи, з яким зустрічаємось при переході від формальної до змістовної моделі, є досить складним і потребує уважного відношення.

Аналогічна ситуація виникає при виборі вхідних величин. Усяка система зв’язана з навколишнім світом безмежною кількістю зв’язків. Які з них слід вибрати як вхідні величини системи? Наприклад, система “Тролейбус”, в якості вхідних величин можуть бути електроенергія, керування, взаємодія з дорогою, пасажири. При більш детальному розгляді необхідно враховувати якість електроенергії, взаємодію струмо-приймача з проводом, зчеплення з дорогою, нахил дороги, нерівності дороги, якість дорожнього покриття, дію опору повітря, атмосферні осадки. Водій, керуючи рухом тролейбуса, користується рулем, гальмами, перемикає світло, переводить ручку контролера. При технічному огляді здійснюють змазку вузлів, регулювання, для чого повинні бути передбачені певні отвори, регулювальні гвинти тощо. Тобто, як ми бачимо, вхідних величин у не самій складній системі, якою є тролейбус, надзвичайно велика кількість. Які ж з них треба включити до системи “Тролейбус”, а які можна не включати? Вхідні величини, як і границі системи, вибирають залежно від контексту, точки зору та цілей моделювання. Без чіткої постановки задач моделювання, обмеження контексту розгляду проблеми відповісти на поставлені вище запитання неможливо. Аналогічна ситуація виникає при виборі вихідних величин.

Модель “чорний ящик” при формальному математичному розгляді може мати представлення системи у вигляді оператора, який діє на вхідні величини і перетворює їх у вихідні. Якщо оператор системи враховує, наприклад, зміну в часі, то такий опис системи буде динамічним. Сам оператор може бути простим чи складним. Він може мати одну або декілька вхідних величин. Може змінюватися в часі, залежати від зовнішніх умов. Отже, як бачимо, модель „Чорний ящик” може бути і надзвичайно складною.

Складність побудови моделі типу “Чорний ящик” полягає ще й у тому, що вона є основою подальшого вивчення системи і розробки конкретних пропозицій для практичної діяльності. На першому етапі аналізу системи можна вибрати або дуже багато вхідних величин, тоді система з простої перетвориться в складну, велику, і вивчити її дуже важко, або вибрати недостатню кількість вхідних величин і система стає спрощеною, вивчення її не дасть практичного результату. Якщо модель служить для цілей розробки певного проекту, для певних практичних рекомендацій, то помилки моделювання і аналізу на початкових етапах виправити пізніше досить важко і коштує це в 10 -100 разів більше. Наприклад, автомобілебудування. У моделі автомобіля на початку його промислового виробництва ніхто не врахував вихлопних газів, теплового випромінювання. Це призвело до виникнення смогу, в якому задихалися, вмирали люди великих міст, до порушення озонового шару Землі, до глобального потепління. Цих явищ могло б не бути, якщо початково в модель були б включені вказані вихідні величини і автомобілебудування їх враховувало. Тепер виправити ці наслідки надто важко.

Модель типу “Чорний ящик” дозволяє подати систему у вигляді оператора R, який перетворює вхідні величини у вихідні. Якщо цей оператор враховує, наприклад, зміну в часі, то такий опис системи буде динамічним. Сам оператор може бути простим чи складним. Він може мати одну або декілька вхідних величин. Може змінюватися в часі, залежати від зовнішніх умов. Отже, як бачимо, модель „Чорний ящик” може бути і надзвичайно складною.

Отже, в підсумку слід відзначити, що модель типу “Чорний ящик” займає досить вагоме місце серед моделей системного аналізу, її побудова є одним з важливих етапів вивчення системи і вирішення проблеми. Побудова моделі є досить складним інтелектуальним завданням, для вирішення якого потрібні глибокі знання проблеми і досвід моделювання.

3. Модель типу “ Склад системи ”

В описі системи “Чорний ящик” цілісність і обмеженість виступають як зовнішні характеристики системи. Ця модель нічого не говорить про те, що являє собою система, з яких підсистем вона складається, як вони взаємодіють. Вона не дає відповіді на запитання про будову системи, її частин, чи інших систем, які входять до її складу. Відповіді на ці запитання дає модель “Склад системи”.

Будь-яка система завжди є складною, неоднорідною У ній існують елементи і навіть самостійні системи (підсистеми). Підсистеми можуть також складатися з елементів та підсистем. Тому при необхідності розглядають ієрархію підсистем, розрізняють підсистеми 1, 2, 3, і т.д. рівня. Формальна модель типу “Склад системи” являє собою прямокутник, який обмежує систему і визначає її границі, і зображення складових частин, елементів та підсистем у границях прямокутника системи. Як правило, підсистеми зображують прямокутником, а елементи колом чи овалом, як це показано на рис. 12.

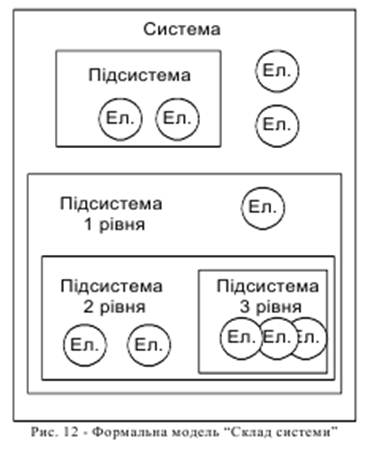
Модель “Склад системи” будують на основі вивчення складових частин системи. На вербальному рівні маємо морфологічний опис (аналіз) системи. Модель „Склад системи” є подальшим розвитком субстрактного аналізу. Цей аналіз залежить від системи, яку вивчаємо, і від цілей моделювання, контексту, рівня знань аналітика. Наприклад, при виконанні морфологічного аналізу системи “тролейбус” виділено складові частини, наведені у табл. 3.

Залежно від цілей аналізу окремі елементи можуть розглядатись як підсистеми. Підсистемою може бути кабіна водія, двері. У підсистему “двері” може входити полотно дверей, вікно, петлі, механізм відкривання та інші елементи, у підсистему “кабіна водія” - сидіння, вікно, руль, панель керування тощо.

Під час побудови змістовної моделі “Склад системи” в першу чергу визначають границі системи, тільки тут їх визначити треба більш чітко ніж при побудові моделі “чорний ящик”, оскільки вони явно входять у модель. Наприклад, система “міський пасажирський транспорт” залежно від цілей моделювання може включати міські магістралі, підрозділи міськвиконкому, підрозділи міліції, які здійснюють керування рухом на міських магістралях, або включати тільки транспортні засоби.

Побудова самої моделі передбачає вирішення питання, як розбити систему на підсистеми і елементи? Елемент – це найменша відмежована, самостійна частина системи, яка при даному розгляді вважається неподільною. Що розуміти під поняттям “елемент системи”? Який рівень підсистем треба врахувати? Відповісти на ці запитання можна по-різному. Побудова змістовної моделі “Склад системи” залежить від:

· цілей моделювання, проблем, які необхідно вирішувати;

· точки зору аналітика;

· контексту вивчення системи;

· ступеня потрібної деталізації;

· рівня знань і досвіду аналітика.
Труднощі побудови моделі мають ряд причин:
По-перше, поняття елемента системи можна розуміти порізному. То, що в одному випадку для вирішення однієї проблеми є елементом, в іншому - складною системою.

По-друге, всяка модель є цільова, а для різних цілей в системі потрібно розглядати різні частини.

По-третє, з різної точки зору система виглядає по-різному. Наприклад, для директора, головного бухгалтера чи інженера заводу складається з різних систем.

По-четверте, усякий поділ є відносним, наприклад, гальмівну систему тролейбуса можна вважати складовою частиною системи керування або ж віднести до ходової частини.

Для успішної побудови моделі “Склад системи” і при виборі підсистем та елементів системи слід виходити із принципу цілісності системи і враховувати умови необхідності та достатності виконаного аналізу.

Принцип цілісності побудови моделі полягає в тому, що модель повинна відображати систему повністю з урахуванням усіх її функцій.

Умова необхідності полягає в тому, що в модель включають тільки елементи, необхідні для виконання системою своїх функцій. Вона дозволяє виявити суттєві елементи й відділити їх від несуттєвих.

Умова достатності полягає у тому, що при побудові моделі враховують чи дозволяють виділені частини в достатній мірі врахувати всі функції системи. Вона забезпечує включення усіх необхідних частин в модель і дозволяє обмежити аналіз його.

Приклад моделі “Склад системи” показано на рис. 13.

Поняття “елемент” - одне з основних в теорії систем. Всяка система незалежно від її природи, має складну будову. Вона складається з різноманітних неоднорідних частин. Кожна частина системи має свої функції, свою будову і свою поведінку. Вона може визначатись як “підсистема” або “елемент” системи залежно від завдань дослідження, контексту розгляду системи. Суть понять “підсистема” і “елемент” дуальна: “підсистема” для частин системи, що знаходяться вище, виступає як елемент, а для частин системи, що знаходяться нижче в структурній ієрархії “підсистема”, - як система.

Елемент – це відносно самостійна частина системи, яка на даному рівні аналізу розглядається як одне ціле зі своєю поведінкою, направленою на реалізацію властивої цьому елементу функції.

Характеристиками елемента є:

- елемент виконує одну чи декілька функцій,

- елемент має свої властивості, свою поведінку,

- елемент використовується у певному контексті. Важливим поняттям є цілісність елемента. Вона залежить від

внутрішніх і зовнішніх факторів. Такими факторами є зв’язки елемента та інтенсивність обміну. Внутрішні фактори - зв’язки та інтенсивність взаємодії частин елемента. Зовнішні фактори – це зв’язки елемента з іншими елементами і взаємодія між ними. Цілісність елемента визначається співвідношенням внутрішніх і зовнішніх факторів. Коли внутрішні фактори переважають над зовнішніми, то елемент є стійким, в іншому випадку він може бути або зовсім нестійким, або мати певну відносну стійкість. У теорії систем ці властивості виражають більш формалізованою мовою на основі математичної теорії множин.

Саме поняття “елемент” трактується подвійно. З одного боку елемент – це абсолютна категорія, що має він конкретний зміст, а з другого - поняття відносне. Поняття “елемент” як абсолютна категорія означає, що це початкова, неподільна, найменша частинка системи. Ми вважаємо, що така частинка існує і в такому відношенні поняття “елемент” має абсолютне значення. З іншого боку, поняття “елемент” є відносне, оскільки пов’язане з рівнем розгляду і деталізації системи із завданнями дослідження. Залежно від цілей розгляду, точки зору елементом може бути та чи інша частина системи, той чи інший її компонент. Із зміною точки зору поняття “елемент” змінюється, тобто категорія “елемент” залежить від розгляду системи і в цьому полягає відносність поняття “елемент”.

4. Модель типу “ Структура системи ”

Розглянуті нами моделі послідовно дозволяють збільшувати ступінь знань про систему. Модель “Структура системи” несе ще більше інформації про систему. Якщо, наприклад, для системи “сім’я” достатньо вказати склад сім’ї, то для характеристики тролейбуса, чи іншої системи одного переліку елементів та підсистем замало. Необхідно ще указати зв’язки між елементами, об’єднати їх в одне ціле, тобто вказати структуру системи.

Під структурою системи розуміють сукупність необхідних та достатніх для досягнення цілі відношень і зв’язків між елементами.

У визначенні системи ми вказували на наявність зв’язків між елементами. У реальних системах зв’язків між елементами безконечна кількість. Кожен природний об’єкт має безліч зв’язків з усіма іншими об’єктами. Зв’язки в системі можуть відігравати суттєву роль чи бути несуттєвими, а інколи і шкідливими. У структурі системи вказують сукупність закономірних, суттєвих зв’язків, що забезпечують функціонування системи.

Для вивчення структури системи використовують два підходи, а саме:

- теорії множин;

- теорії графів.

У теорії множин структуру виражають відношеннями між елементами.

Теорія розглядає подвійні, потрійні та інші відношення, їм у відповідність ставляться бінарні відношення, добутки елементів. У теорії множин структуру системи описують за допомогою матриць суміжності. Матриця суміжності - це математичний об’єкт зображений у вигляді прямокутної матриці, елементи якої встановлюють зв’язки і відношення між складовими частинами системи. Як правило, матриці суміжності, що описують структуру системи, є розрідженими матрицями, тобто матрицями великих розмірів, значна кількість елементів якої дорівнює нулю.

Теорія множин розглядає множини вхідних і вихідних процесів, рівняння, що установлюють зв’язки між множинами вхідних і вихідних величин за допомогою операторів переходу. Теоретикомножинний підхід до вивчення теорії систем математично досить розвинений.

Більш простим і менш формалізованим є підхід теорії графів. Зображення структури подається у вигляді графа. Граф структури системи встановлюють шляхом декомпозиції системи і вивчення зв’язків між складовими частинами.

Формальна модель “Структурна схема” - це, як правило, зображення системи у вигляді графа, хоча під час теоретичного вивчення може бути і матриця сумісності. Ми в якості формальної моделі “Структура системи” будемо розглядати певний граф. Ця модель включає в себе елементи системи, зображені точками чи кружками і зв’язки між ними зображені лініями або лініями зі стрілками. Як елементи в моделі “Структурна схема” розглядають всі складові частини системи, не розрізняючи, підсистема це чи елемент, як це було в моделі “Структурна схема”.

Графом G називають деяку сукупність пар елементів вершин і ребер. Вершини зображають у вигляді точки, ребра – лініями.

Розглянемо деякі поняття теорії графів.

Підграф – підграфом граф G називають граф, всі вершини і ребра якого знаходяться серед вершин і ребер графа G.

Направлений граф – це такий граф, ребра якого мають напрямок.

Ненаправлений граф – граф, у якому напрямок ребер не відіграє ролі або його неможливо визначити.

Зв’язаний граф – це граф, у якого для всяких двох різних вершин існує послідовний ланцюг вершин і ребер, що їх з’єднує.

Зважений граф – це граф, у якому всім ребрам ставиться у відповідність певне число.

Циклом називають будь-яку замкнуту послідовність вершин і ребер.

Деревом називають граф, у якого відсутні цикли.

Остовом графа G називають дерево, в яке входять усі вершини графа G.

Поняття теорії графів широко використовуються при аналізі структури системи. Структура системи відображає зв’язки між елементами. При розгляді структури елементами системи вважають усі складові частини, не виділяючи окремих підсистем, тобто у моделі структури системи підсистему вважають елементом. Структуру системи зображають у вигляді графа. Вигляд графа структури описують його топологією.

Граф може мати таку топологію:

· лінійну,

· кільцеву,

· ієрархічну,

· деревовидну,

· сіткову,

· матричну.
Вигляд структур, що відповідають вказаній топології, показаний

на рис. 14.

Лінійна структура – це структура, в якій кожна вершина зв’язана тільки з двома іншими вершинами і є дві крайні вершини. У системах вона зустрічається часто, наприклад, на виробництві: виготовлення заготовки, послідовні операції обробки, технічний контроль деталі утворюють лінійну структуру. У системі “Тролейбус” лінійна структура відповідає передачі електричної енергії від приймальної штанги до електродвигуна.

Кільцева структура – це лінійна структура, в якій крайні вершини зв’язані між собою. Кільцева структура описує, наприклад, обіг грошей у фінансових організаціях. Вона характерна для технологічних операцій, коли цикл виробництва повторюється багаторазово. У тролейбусі кільцеві структури описують, наприклад, роботу гідросистеми. Системи охолодження двигуна автомобіля також має кільцеву структуру. В природі це кругообіг води, зміна пір року.

Ієрархічні структури – це структури, в яких елементи розміщені на різних рівнях, причому елементи -го рівня підпорядковані елементам -1 рівня і впливають на елементи +1 рівня. Різновиди ієрархічних іі структур будуть розглянуті в подальшому. Найчастіше вони зустрічаються під час аналізу організаційних систем, в яких є чітка структура підпорядкування. Типовий приклад це структура підпорядкування в армії. Ієрархічна структура може описувати і будову багатьох складних систем, рівнями яких є підсистеми, як, наприклад, ми це бачили при розгляді моделі “Склад системи”.

Для ієрархічних систем зв’язки між елементами можуть мати координаційний та субординаційний характер. Координаційний характер мають зв’язки між елементами, що знаходяться на одному рівні, субординаційні – між елементами різного рівня.

Деревовидна структура – це ієрархічна структура, в якій відсутні цикли.

Сітьова структура – це різновид ієрархічної структури, в якій можливі зв’язки через декілька рівнів і допускається наявність циклів. Вона характерна для розробки графіків роботи підприємств, технологічних операцій збирання складних виробів тощо.

Під час виконання системного аналізу для складних систем, особливо організаційних систем будують декілька структур: структуру керування, структуру виробництва, структуру функціонування та ін. Вони, як правило, бувають різної топології: структура керування – ієрархічна, структура функціонування – лінійна чи кільцева, структура технологічного процесу – сіткова тощо.

5. Модель “ Структурна схема системи ”

Ця модель являє собою сукупність розглянутих вище трьох типів моделей, а саме: “Чорний ящик”, “Склад системи” і “Структура системи”. Вона є найбільш детальною та повною моделлю системи. ЇЇ зображують також у вигляді графа, але вузли його, як правило, наповнюють певним змістом, зображають прямокутником, еліпсом чи колом. У моделі “Структурна схема системи“ показують:

· границі системи,

· елементний склад системи,

· зв’язки між окремими елементами,

· зовнішні зв’язки системи.

Формальна модель “Структурна схема” містить елементи системи, зображені, як правило, прямокутниками чи еліпсами, в середині яких записана назва елемента і зв’язки між елементами показані лініяи чи стрілками. Ця модель здобула широке міждисциплінарне визнання. Її використовують в різних наукових дисциплінах, технічних організаційних та інших документах. Тому існує багато особливостей зображення складових частин на моделі “Структура системи”. Так, часто зовнішні границі системи на цій моделі не показують, назву системи записують як заголовок чи підпис до моделі, елементи зображають на різних рівнях і по–різному позначають, зв’язки між елементами показують лініями різних типів, стрілками, у вигляді шин та ін. Модель “Структурна схема” системи примикає до великої різноманітності моделей, кожна з яких має своє призначення і свої особливості.

Модель “Структурна схема” деколи називають моделлю “Білий ящик”, розуміючи під цим визначенням те, що на противагу моделі “Чорний ящик” у ній повністю показана внутрішня будова системи.

Модель “Структурна схема”, як і інші моделі, залежить від точки зору, цілей аналізу, контексту розгляду системи, тому таких моделей може бути велика кількість. Як правило, для системи будують кілька моделей, що відображає різноманітність зв’язків у системі, різні підходи до вивчення системи, різні контексти її розгляду.

6. Динамічні моделі

Це моделі, що зображають динаміку системи. Розрізняють такі різновиди динаміки:

- функціонування,

- зростання,

- розвиток.

Моделі функціонування відображають процеси, що відбуваються в системі і направлені на виконання системою своїх функцій та досягнення цілей.

Моделі зростання і розвитку системи дозволяють простежити розвиток системі протягом деякого більш тривалого проміжку часу. Слід зауважити, що процеси зростання і розвитку не є тотожними. Зростання систем, як правило, пов’язане із збільшенням їх розмірів, включенням в систему деяких об’єктів із зовнішнього середовища, матеріальних та інших ресурсів. Наприклад, зростання підприємства при збільшенні об’єму випуску продукції полягає в побудові нових виробничих корпусів, закупівлі додаткового обладнання, залученні до роботи більшого числа робітників. На противагу цьому розвиток може здійснюватись без збільшення розмірів системи, а інколи навіть при її зменшенні. Наприклад, розвиток сучасних підприємств часто відбувається без збільшення їх розмірів. Розвиток - це така зміна системи, при якій змінюються зв’язки між елементами, спрощуються відношення, удосконалюється виконання окремих функцій. Наприклад, розвиток сучасної автомобілебудівної промисловості, металургії та ін. супроводжується удосконаленням технологічних процесів, випуском більш надійних якісних товарів без помітного розширення підприємств. Як правило, розвиток супроводжується глибокою зміною внутрішньої організації системи, зміною її структури.

Динаміку систем вивчають з використанням математично - множинних методів, засновуючись на положеннях теорії множин. Ди­наміка системи описується як перехід з одного стану в інший. Сукуп­ність можливих станів системи називають множиною станів. Системи можуть мати дискретні стани (система може знаходитись тільки в пев­них, дозволених станах) або неперервні стани (система переходить послідовно з одного стану в інший через безконечну кількість проміж­них станів). Зображення можливих станів системи здійснюється у про­сторі станів. Це, як правило, абстрактний математичний простір. Опи­сати динаміку системи в просторі станів можна матрицями суміжності або за допомогою графів. Для вивчення динаміки систем використо­вують множини вхідних і вихідних процесів. Динаміку системи розглядають як послідовний перехід системи з одного стану в інший. Теоретико-множинні методи вивчення динаміки систем спрямовані на вивчення керованості системи, стійкості, надійності функціонування., вивчення роботи в даний момент часу і прогнозу розвитку системи в майбутньому. На основі теоретичних розрахунків встановлено, що системи можуть бути безсмертними чи смертними. Для того щоб сис­тема існувала вічно, була безсмертною необхідно, щоб вона розширю­валась. Встановлена теорема, згідно з якою система була б вічною, потрібно щоб зростання елементів у системі не відставало від логари­фмічного закону.

Деякі питання динаміки систем можна спрощено продемонстру­вати, якщо представити модель системи у вигляді оператора, який пе­ретворює вхідні величини у вихідні.

Наприклад,

y (t) = R[x(t)].

Тут R - оператор системи, який діє на вхідну величину x(t). Величина x(t) може розглядатись, як одна одновимірна вели­чина, або як вектор, тобто сукупність величин x₁(t), x2(t), x₃(t)...

Це ж відноситься і до вихідної величини y (t).

Наведене рівняння описує найбільш просту систему, вихідна величина залежить тільки від значення вхідної величини в кожний мо­мент часу t.

Більш складною є залежність

y (t) = R[x(t), z],

яка описує дещо складнішу стаціонарну систему. Вихідна величина

залежить від вхідної і параметра системи z. Наступне рівняння таке:

y (t) = R[x(t), z(t)], описує нестаціонарну систему: вихідна величина залежить від вхідної і

параметра системи z(t), який змінюється протягом часу.

Рівняння ще більш складної динамічної системи можна записа­ти так:

y (t) = R[x(t, t-М), z (t)].

Це вже нестаціонарна інерційна система або система з пам’яттю, в ній вихідна величина залежить від значень вхідної вели­чини не тільки в даний час, але й від попередніх значень.

7. Моделі зовнішнього середовища

Розглянуті нами моделі є найбільш вживаними при виконанні системного аналізу. Вони описують систему. Для повноти аналізу їх доповнюють моделями зовнішнього середовища. Ці моделі відобра­жають контекст розгляду проблеми. Як правило, будують декілька моделей зовнішнього середовища, а саме: модель середовища прямої дії і модель середовища опосередненої дії, модель властивостей сере­довища. На цих моделях систему, як правило, зображують у вигляді еліпса, а зовнішні по відношенню до неї системи у вигляді прямокут­ників, або прямокутників із тінню, щоб підкреслити той факт, що вони знаходяться в іншій площині, ніж система, яка вивчається. Середови­ще прямої дії - це ті навколишні системи, з якими безпосередньо взає­модіє система. Середовище опосередненої дії - це системи, безпосере­дньо з якими дана система не взаємодіє, але вони через існуючі зв’язки впливають на функціонування системи.

Крім цього, у вигляді окремої моделі приводять властивості зо­внішнього середовища. Такими властивостями є складність середови­ща, його рухомість, ступінь визначеності, взаємозв’язок факторів се­редовища. Приклад моделі середовища наведений на рис. 15.

14.Які моделі відносять до формальних моделей, яке їх значення в системному аналізі?

15.Що розуміють під поняттям “змістовна модель”?

16.Як Ви розумієте поняття “інтерпретація”, в якій мірі воно відноситься до змістовних моделей?

17.Чим обмежена кількість формальних і змістовних моделей? Що являє собою формальна модель типу “Чорний ящик”? Яке значення моделі типу “Чорний ящик” у системному аналізі”?

18.Наведіть приклади використання моделі типу “Чорний ящик” у різних наукових дисциплінах.

19.У чому полягають труднощі побудови змістовної моделі ти-пу “Чорний ящик”?

20.Опишіть формальну модель типу “Склад системи”.

21.Що розуміють під поняттям “елемент системи”?

22.Який рівень підсистем треба врахувати під час системного аналізу?

23.Дайте визначення поняттю “елемент”.

24.У чому полягає відносність поділу системи на підсистеми і елементи?

25.У чому полягає умова необхідності й достатності під час
побудови моделі “Структура системи”.

26.Назвіть основні характеристики елемента.

27.У чому полягає використання підходу теорії множин для опису структури системи?

17.Що являє собою матриця суміжності, для чого її використо-вують у системному аналізі?

18.Дайте визначення поняттю “граф”.

19.Який граф називають деревом?

20.Що розуміють під поняттям топологія графа?

21.Які типи топологій графа Ви знаєте?

22.Дайте визначення ієрархічної структури.

23.Опишіть формальну модель “Структурна схема“.

24.Що розуміють під поняттям “динаміка системи”?

25.Які різновиди динаміки Ви знаєте?

26.Що входить в середовище прямої дії?

27.Що входить в середовище опосередненої дії?

28.Які властивості зовнішнього середовища Ви знаєте?

Дата добавления: 2014-01-15