Постановка задачи. Эмпирические функции регрессии

Эмпирические функции регрессии

При экспериментальном изучении функциональной зависимости одной величины (y) от другой (x) проводят ряд измерений величины y при различных значениях величины х.

Предположим, что изучается зависимость (Пример Спросить у О.В.) yjvb номинальной мощности автомобильного двигателя от устанавливаемого угла опережения зажигания (УОЗ). Для этого устанавливают минимальный УОЗ (при котором двигатель будет еще работать), запускают двигатель и на стенде тяговых качеств определяют номинальную мощность. Затем увеличивают УОЗ на один или несколько градусов (в зависимости от программы эксперимента) и снова определяют номинальную мощность. Опыты проводят до того момента, пока УОЗ не станет равным максимальному.

Результаты экспериментов можно представить графически (рис. 2.1) или в табличном виде (табл. 2.1).

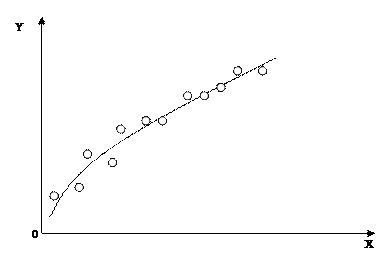
Рисунок 2.1 – Графическое представление результатов однофакторного эксперимента.

Однако, такие формы представления результатов не позволяют четко представить характер зависимости данных величин – аргумента и функции. Это можно сделать только на основе полученной аналитической зависимости, достаточно хорошо описывающей результаты эксперимента.

Таблица 2.1 –Результаты однофакторного эксперимента в табличном виде

УОЗ (x)	x1	x2	…	xi	…	xn
Номинальная мощность (Y)	y1	y2	…	yi	…	yn

Таким образом, ставится задача аналитического представления искомой функциональной зависимости. Адекватность модели?????????

Сложность задачи заключается в том, что наличие случайных ошибок измерения (как говорят наличие «шумов» в эксперименте) делает нецелесообразным подбор такой функции, которая точно описывала бы все опытные значения, т.е. график не должен проходить через все точки, а по возможности должен сглаживать «шум». Сглаживание будет тем больше и надежнее, чем больше количество проведенных экспериментов.

Например, для проведения прямой y=a0+a1*x необходимы две точки: (х1,y1) (x2,y2) если они известны точно. А для проведения более сложной аналитической зависимости при наличии значительного «шума» может понадобиться и большее количество экспериментальных точек.

Посмотреть:

Колесников А., Excel 2000- К.: Издательская группа BHV, 1999 –496с.: ил

А.В. Кузнецов, В.А.Сакович, Н.И. Холод. Высшая математика. Математическое программирование., Минск, «Вышэйшая школа», 1994г.286 с., ил

Б.П. Демидович, И.А. Марон и др. Численные методы анализа., М:, «Наука», 1967г., 368с.,

Итак, имеются наблюдаемые значения случайной величины (СВ) - точки (x_i,y_i) i=1,…,n. Если аналитическое выражение зависимости y от x неизвестно, то возникает практически важная задача: выбрать по статистическим данным (x_i,y_i) i=1,…,n общий вид эмпирической функции регрессии y=f(x), значения которой при х=х_i возможно мало отличались бы от опытных данных y_i.(рисунок 2.1).

Построение эмпирической функции регрессии слагается из двух этапов:

1. Выяснение общего вида этой формулы

2. Определение наилучших параметров её.

В некоторых случаях выбор эмпирической функции регрессии может быть произведен геометрически. Т.е. подобрать такую формулу, которая лучше подходит к кривой, построенной по данным наблюдений.

Это могут быть степенные (y=a*x ^b), логарифмические (y=a*Ln(x)+b), экспоненциальные (y=a*e ^b*x ) ит.п.

Если неизвестен характер зависимости между величинами x_i,y_i, то вид эмпирической функции регрессии является произвольным.

Во многих случаях можно ограничиться многочленом. (Любой вид зависимости путем преобразований можно привести к многочлену.)

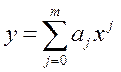
При построении эмпирической функции регрессии можно предположить, что исходные данные x_i,y_i (i=1,…,n) положительны.

Действительно, если бы например:

· Все x_i < 0 (или все y_i< 0), то достаточно рассмотреть таблицу значений - x_i, y_i (или соответственно x_i, - y_i)

· Все x_i и y_i < 0. Тогда достаточно построить эмпирическую функцию регрессии для таблицы - x_i, - y_i.

· Знаки x_i, y_i – переменные, т.е. имеем общий случай. Т.к. таблица значений x_i, y_i конечна, то всегда можно подобрать числа «m» и «n» такие, что

ξ_i = m+ x_i, η_i = n+ y_i

Отсюда получаем, что решение поставленной задачи сводится к нахождению эмпирической функции регрессии для системы положительных значений ξ_i, η_i

Если вид эмпирической функции регрессии выбран, то возникает задача определения наилучших коэффициентов (параметров), входящих в эту формулу.

Т.о. задача ставится следующим образом.

Пусть дана совокупность пар значений (x_i,y_i) i=1,…,n, которая приближённо описывается формулой вида

(2.1)

где f - известная функция, и a₀,a₁,a₂,...,a_m – параметры эмпирической функции регрессии, которые необходимо определить.

Т.е. нужно найти наилучшие значения a₀,a₁,a₂,...,a_m, приближенно удовлетворяющие системе уравнений

y_i = f(x_i, a₀,a₁,a₂,...,a_m), i=1,…,n (2.2)

и такие, что невязки (уклонения)

y_i- f(x_i, a₁,a₂,...,a_m)=e_i (i=1,…,n) (2.3)

являются, возможно, малыми по абсолютной величине.

Для определения параметров a₀,a₁,a₂,...,a_m применяются методы

· Метод выбранных точек

· Метод средних

· Метод наименьших квадратов

Остановимся на методе наименьших квадратов, т.к. он имеет наилучшую сходимость.

Дата добавления: 2014-01-15