Метод наименьших квадратов

Остановимся на методе наименьших квадратов, т.к. он имеет наилучшую сходимость.

Метод наименьших квадратов Гаусс разработал в 1794 г., но опубликовал его только в 1808 г.

На два года раньше, а именно в 1806 г., Лежандр в своем мемуаре «Новый способ определения орбит комет» также предложил этот метод, но его изложение не такое полное, как у Гаусса. Гаусс и позднее неоднократно возвращался к изложению своего метода и довел его до полной законченности и совершенства.

Из многочисленных применений метода наименьших квадратов мы рассмотрим только наиболее важное, которое относится к определению наилучшего уравнения заданного типа для представления наблюденных данных, т. е. для обработки результатов наблюдений.

Согласно методу наименьших квадратов (МНК) наилучшими коэффициентами а₀, a₁,a₂,...,a_m считаются те, для которых сумма квадратов уклонений наблюдаемых значений переменной y_i от соответствующих ординат эмпирической функции регрессии y=f(x_i, a₀,a₁,a₂,...,a_m) будет минимальной, т.е.

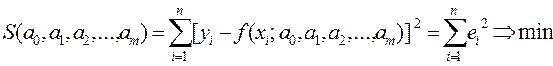(2.4)

Отсюда, используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему для определения коэффициентов a₁,a₂,...,a_m.

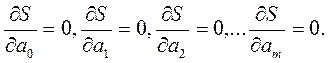(2.5)

Если система имеет единственное решение, то оно будет искомым.

Метод наименьших квадратов обладает тем преимуществом, что если сумма квадратов уклонений 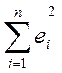мала, то сами эти уклонения малы по абсолютной величине.

Недостатком метода наименьших квадратов, является громоздкость вычислений. Поэтому к нему прибегают обычно при обработке наблюдений высокой точности, когда нужно получить весьма точные значения параметров.

Рассмотрим методику расчёта эмпирических функций регрессии методом наименьших квадратов для линейной зависимости. Предположим, что произведён эксперимент, в результате которого зафиксировано «n» значений исследуемых переменных X и Y (x_i, y_i,, i=1,…,n). Нанося экспериментальные данные в виде точек в декартовой системе координат, получаем корреляционное поле, изображенное на рисунке 1.2

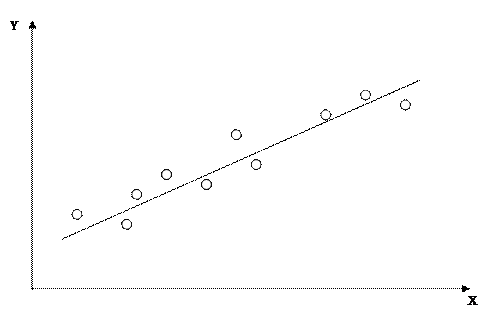
Рисунок 2.2 - Корреляционное поле эксперимента.

Если точки на корреляционном поле группируются вокруг прямой линии, то эмпирическая функция регрессии изображается в виде

y =f(x,a₁,a₂)=a₁+a₂x..

Следующая задача – нахождение параметров a₁,a₂. Находим их методом наименьших квадратов при условии

(2.6)

Для этого находим частные производные

(2.7)

Раскрывая скобки и выполняя элементарные операции, получим систему из двух линейных уравнений, называемых нормальными уравнениями

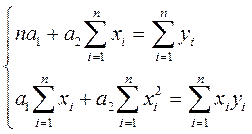(2.8)

Решая систему, находим a₁,a₂.

Пример.

Имеются две наблюдаемые величины x и y, например, объем реализации фирмы, торгующей подержанными автомобилями, за шесть недель ее работы. Значения этих наблюдаемых величин приведены в таблице 2.2, где х – отчетная неделя, а y – объем реализации за эту неделю.

Необходимо найти эмпирическую функцию регрессии y =f(x,a₁,a₂) по шести парам наблюдаемых значений СВ (X,Y)

Таблица 2.2 – Значения наблюдаемых величин

x
y

Если нанесем точки на декартову систему координат, то заметим, что они группируются вокруг прямой линии. Поэтому будем подбирать эмпирическую функцию регрессии линейного вида y= a₁+a₂x. Для удобства все вычисления расположим в таблице (таблица 1.2).

Y

Рисунок 2.3 – Результаты эксперимента

Таблица 2.3 – Значения коэффициентов

xi	yi	xi yi	xi^2
Суммы

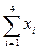
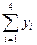
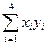
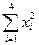
В результате получится система уравнений для нахождения коэффициентов a₁,a₂

6а₁ + 21а₂ = 72

21 а₁ + 91 а₂ = 285

Решая систему получим а₁ = 5,4 и а₂ = 1,885714.

Тогда эмпирическая функция регрессии будет иметь вид

y = 5,4 + 1,885714 x

В наше время существует большое количество специализированных программных пакетов (MathCad, Statistica, MathLab и т.д.), позволяющих производить различные статистические вычисления, оценивать полученные результаты по различным критериям.

До сих пор мы говорили об уравнениях регрессии, когда строим зависимость между функцией и одной переменной, т.е.

y=f(x). (2.9)

Такая зависимость называется парной.

Как правило, на любой рассматриваемый объект или процесс оказывает влияние гораздо большее количество факторов. Так, например, на мощность автомобильного бензинового двигателя помимо угла опережения зажигания влияют и другие факторы (температура охлаждающей жидкости, зазор между электродами свечей зажигания, износ цилиндропоршневой группы и т.д.). Поэтому мы можем говорить о многофакторной задаче.

Дата добавления: 2014-01-15