Матричная модель МОБ СНС

На базе таблиц "затраты-выпуск" могут быть построены матричные модели Леонтьева или модели "затраты-выпуск", которые в России называются моделями МОБ СНС в стоимостном выражении имеет следующий вид:

Общая схема межотраслевого баланса

Промежуточное потребление

Личное потреб-ление

Колек-тивное потреб-ление

Общест-венное потребление

Капитало- образование

Сальдо экспорт-импорт

Итого

В сфере материального производства

В сфере нематериальных услуг

Сфера материаль-ного производства

      I квадрант  

   

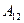II квадрант  

   

   

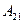
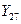
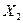
Сфера нематериаль-ных услуг

Амортизация основных фондов

 

	III квадрант

Чистый доход

Итого

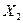
I квадрант содержит данные о промежуточном потреблении. Это квадратная таблица с отраслями по строкам и столбцам. В столбцах по каждой отрасли представлены затраты на производст­во продуктов по отраслям экономики, а по строкам показывается, как распределяются продукты каждой отрасли между всеми отрас­лями.

II квадрант отражает конечное использование. Здесь строки соответствуют отраслям - производителям, а столбцы – основным направлениям конечного использования: конечное потребление, валовое накопление и экспорт. Итог по строкам квадранта показы­вает общее конечное использование, а по строке I и II квадранта - общее использование.

III квадрант показывает стоимостную структуру ВДС. Он со­держит данные как о первичных затратах в каждой отрасли, так и об общих ресурсах по каждому продукту. В верхней части этой табли­цы столбцы соответствуют отраслям-производителям, а строки -
основным компонентам добавленной стоимости (оплата труда, чис­тая прибыль, потребление основного капитала, чистые налоги, от­носящиеся к производству). В нижней части таблицы столбцы соот­ветствуют продуктам, произведенным каждой отраслью, а строки показывают условные переброски продуктов из одной отрасли в другую, которые позволяют перейти от данных о фактическом вы­пуске данной отрасли к данным о распределенном выпуске продук­тов (побочные продукты, смежные продукты и случайные продажи), импорте и о таких различных статьях, как торгово-транспортная наценка, налоги и, наконец, итог ресурсов.

Таким образом, по столбцам межотраслевого баланса показы­вается стоимостная структура валового выпуска отдельных отраслей, которая состоит из промежуточного потребления (I квадрант) и валовой добавленной стоимости (III квадрант). По строкам показано использование продуктов на промежуточное потребление (I квад­рант) и конечное использование (II квадрант).

По строке таблицы мы рассматриваем использование:

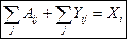
- межотраслевые потоки

Промежуточное потребление + ВВП = валовой выпуск

По столбцу даются ресурсы:

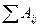- промежуточное потребление + амортизация + чистый доход = валовой выпуск

В матричной форме эта модель будет иметь вид:

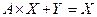
А – матрица коэффициентов прямых затрат, размерностью , где - количество отраслей.

Х – вектор валового выпуска

Y – вектор конечной продукции

- коэффициен6ты прямых затрат, показывающие сколько продукции -ой отрасли (валовой выпуск) требуется для производства единицы продукции -ой отрасли (валовой выпуск)

Уравнение строки:

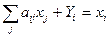
Уравнение столбца:

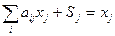
S – добавленная стоимость

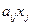называется межотраслевыми потоками

Свойства коэффициентов прямых затрат

1)

2) (сумма по столбцу)

3) с точки зрения экономического смысла 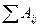- доля промышленного потребления (сырья, материалов) в стоимости продукции. Математически это выглядит следующим образом:

Разделим уравнение столбца на и получаем:

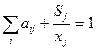
Вернемся к уравнению межотраслевого баланса в матричной форме, выразим:

либо относительно Х

либо относительноY

,

где Е – единичная матрица

Задавшись валовым выпуском, мы можем определить вектор конечной продукции.

По ретроспективным данным рассчитывается .

Решим уравнение МОБ относительно Х:

Задавшись вектором конечной продукции можно определить вектор валового выпуска или:

,

где - называется матрицей коэффициентов полных затрат

Уравнение строки в последнем уравнении будет выглядеть как:

Дифференцируя уравнение строки по 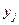, получаем:

,

т.е. коэффициент полных затрат показывает сколько продукции -ой отрасли (валовой выпуск) требуется для производства единицы конечной продукции -ой отрасли

Матрица В может быть получена также разложением в ряд:

Поскольку ряд будет сходящимся.

Дата добавления: 2014-01-15